题目内容
【题目】已知椭圆![]() :
:![]() 的左、右顶点分别是双曲线
的左、右顶点分别是双曲线![]() :
:![]() 的左、右焦点,且
的左、右焦点,且![]() 与
与![]() 相交于点(
相交于点(![]() ).
).
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() :
:![]() 与椭圆
与椭圆![]() 交于A,B两点,以线段AB为直径的圆是否恒过定点?若恒过定点,求出该定点;若不恒过定点,请说明理由.
交于A,B两点,以线段AB为直径的圆是否恒过定点?若恒过定点,求出该定点;若不恒过定点,请说明理由.
【答案】(1)![]() (2)以线段AB为直径的圆恒过定点
(2)以线段AB为直径的圆恒过定点![]() .
.
【解析】
(1)根据点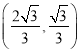 在双曲线
在双曲线![]() 上,求出
上,求出![]() ,由椭圆
,由椭圆![]() 的左右顶点是双曲线
的左右顶点是双曲线![]() 的左右焦点可求出
的左右焦点可求出![]() ,最后由点
,最后由点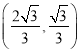 也在椭圆
也在椭圆![]() 上求得
上求得![]() .
.
(2)先把直线方程与椭圆方程联立,消去![]() ,得到关于
,得到关于![]() 的一元二次方程,利用根据系数的关系得到
的一元二次方程,利用根据系数的关系得到![]() ,
,![]() 两点的横坐标关系.根据圆上任意一点到直径端点的构成的两个向量垂直,即数量积为0,则可求出以线段AB为直径的圆恒过定点.
两点的横坐标关系.根据圆上任意一点到直径端点的构成的两个向量垂直,即数量积为0,则可求出以线段AB为直径的圆恒过定点.
解:(1)将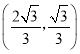 代入
代入![]()
解得![]() ,
,![]() .
.
将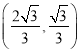 代入
代入![]() 解得
解得![]() ,
,
![]() 椭圆
椭圆![]() 的标准方程为:
的标准方程为:![]() ;
;
(2)设![]() ,
,
由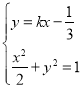 整理得
整理得
![]() ,
,
![]()
![]()
法一:由对称性可知,以AB为直径的圆若恒过定点,是定点必在y轴上.
设定点为![]() ,则
,则
![]()
![]()
![]()
![]()
![]()
![]()
![]()
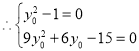 ,解得
,解得![]() ,
,![]()
![]() 以线段AB为直径的圆恒过定点
以线段AB为直径的圆恒过定点![]()
法二:设定点为![]() ,则
,则
![]()
![]()
![]() …
…
![]()
![]()
![]()
![]()
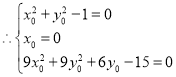 解得
解得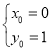 ,
,![]()
![]() 以线段AB为直径的圆恒过定点
以线段AB为直径的圆恒过定点![]() .
.

练习册系列答案
相关题目