题目内容
直线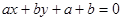 与圆
与圆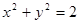 的位置关系为( )
的位置关系为( )
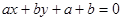 与圆
与圆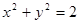 的位置关系为( )
的位置关系为( )| A.相交 | B.相切 | C.相离 | D.相交或相切 |
D
分析:由圆的方程找出圆心坐标与半径r,利用点到直线的距离公式表示出圆心到已知直线的距离d,比较d与r的大小即可得到直线与圆的位置关系.
解答:解:由题设知圆心到直线的距离d= ,
,
而(a+b)2≤2(a2+b2),
得d≤ ,圆的半径r=
,圆的半径r= ,
,
所以直线ax+by+a+b=0与圆x2+y2=2的位置关系为相交或相切.
故选D
点评:此题考查学生灵活运用点到直线的距离公式化简求值,掌握直线与圆位置关系的判别方法,是一道基础题.
解答:解:由题设知圆心到直线的距离d=
 ,
,而(a+b)2≤2(a2+b2),
得d≤
 ,圆的半径r=
,圆的半径r= ,
,所以直线ax+by+a+b=0与圆x2+y2=2的位置关系为相交或相切.
故选D
点评:此题考查学生灵活运用点到直线的距离公式化简求值,掌握直线与圆位置关系的判别方法,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
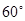 的直线被圆
的直线被圆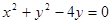 所截得的弦长为( )
所截得的弦长为( )



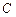 方程为:
方程为: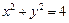 .
.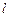 过点
过点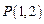 ,且与圆
,且与圆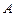 、
、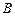 两点,若
两点,若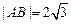 ,求直线
,求直线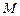 作平行于
作平行于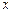 轴的直线
轴的直线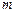 ,设
,设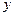 轴的交点为
轴的交点为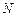 ,若向量
,若向量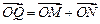 (
(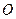 为原点),求动点
为原点),求动点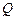 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线. N(1,0)的距离的比为。
N(1,0)的距离的比为。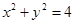 所截弦的中点的轨迹为C,则曲线C与直线
所截弦的中点的轨迹为C,则曲线C与直线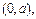 其斜率为1,且与圆
其斜率为1,且与圆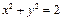 相切,则
相切,则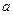 的值为( )
的值为( )




 :
: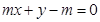 交圆C:
交圆C: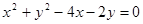 于
于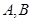 两点,当
两点,当
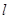 的方程是( )
的方程是( )



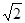 ,AD=
,AD=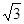 ,则∠CAD的弧度数为 .
,则∠CAD的弧度数为 .