题目内容
(12分)已知点P到两个定点M(-1,0), N(1,0)的距离的比为。
N(1,0)的距离的比为。
(1)求证点P在一定圆上,并求此圆圆心和半径;
(2)若点N到直线PM的距离为1,求直线PN的方程。
 N(1,0)的距离的比为。
N(1,0)的距离的比为。(1)求证点P在一定圆上,并求此圆圆心和半径;
(2)若点N到直线PM的距离为1,求直线PN的方程。
解:(1)设P点坐标为(x,y),根据已知条件可得|PM|∶|PN|= .即
.即
= ,整理得x2+y2-6x+1
,整理得x2+y2-6x+1 =0.①
=0.①
圆心坐标为(3,0),半径
(2)设PM的方程为y=k(x+1),即kx-y+k=0.
由N到PM的距离为1得 =1,解得k=±
=1,解得k=± .
.
∴y= (x+1),②
(x+1),②
或y=- (x+1).③
(x+1).③

∴P点坐标为(2+ ,
, +1)、(2-
+1)、(2- ,
, -1)、(2+
-1)、(2+ ,-
,- -1)、
-1)、
(2- ,1-
,1- ).
).
因此所求直线PN的方程为x-y-1=0或x+y-1=0.
 .即
.即
=
 ,整理得x2+y2-6x+1
,整理得x2+y2-6x+1 =0.①
=0.①圆心坐标为(3,0),半径

(2)设PM的方程为y=k(x+1),即kx-y+k=0.
由N到PM的距离为1得
 =1,解得k=±
=1,解得k=± .
. ∴y=
 (x+1),②
(x+1),②或y=-
 (x+1).③
(x+1).③
∴P点坐标为(2+
 ,
, +1)、(2-
+1)、(2- ,
, -1)、(2+
-1)、(2+ ,-
,- -1)、
-1)、 (2-
 ,1-
,1- ).
).因此所求直线PN的方程为x-y-1=0或x+y-1=0.
略

练习册系列答案
相关题目
 b,且a
b,且a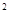 sin
sin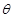 +acos
+acos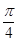 ="0" ,b
="0" ,b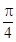 =0,则连接(a,a
=0,则连接(a,a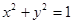 的位置关系是( )
的位置关系是( )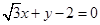 截圆
截圆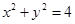 得到的弦长为( )
得到的弦长为( )



 与曲线
与曲线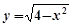 有两个交点,则k的取值范围是
有两个交点,则k的取值范围是 )
)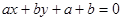 与圆
与圆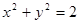 的位置关系为( )
的位置关系为( ) =a,
=a, =b(a>2,b>2).
=b(a>2,b>2).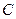 :
: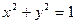 和
和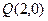 ,动点
,动点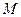 到圆
到圆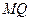 |的比等于常数
|的比等于常数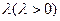 ,求动点
,求动点 得的劣弧所对的圆心角为
得的劣弧所对的圆心角为  置关系是
置关系是