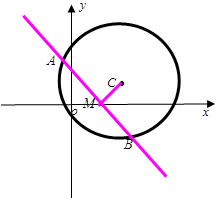
题目内容
已知直线 :
: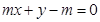 交圆C:
交圆C: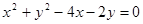 于
于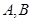 两点,当
两点,当
最短时,直线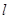 的方程是( )
的方程是( )
 :
: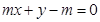 交圆C:
交圆C: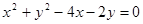 于
于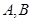 两点,当
两点,当
最短时,直线
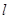 的方程是( )
的方程是( )A. | B. | C. | D. |
A
本题考查直线与圆的位置关系..
由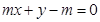 得
得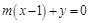 ,则直线
,则直线 恒过定点
恒过定点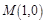 ,直线
,直线 的斜率
的斜率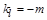 ;
;
因为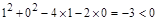 ,所以点
,所以点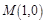 在圆C内。
在圆C内。
又由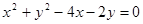 得
得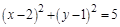 ,即圆C的圆心为
,即圆C的圆心为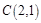 ,半径为
,半径为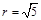 ;
;
由垂径定理知,当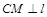 时弦最短,此时有
时弦最短,此时有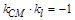
因为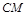 的斜率为
的斜率为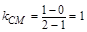 ,所以
,所以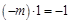 ,则
,则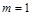 ,
,
所以所求直线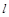 的方程为
的方程为
故正确答案为A
由
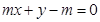 得
得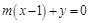 ,则直线
,则直线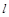 恒过定点
恒过定点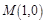 ,直线
,直线 的斜率
的斜率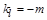 ;
;因为
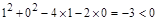 ,所以点
,所以点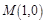 在圆C内。
在圆C内。又由
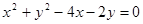 得
得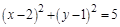 ,即圆C的圆心为
,即圆C的圆心为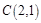 ,半径为
,半径为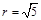 ;
;由垂径定理知,当
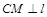 时弦最短,此时有
时弦最短,此时有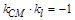
因为
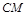 的斜率为
的斜率为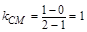 ,所以
,所以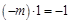 ,则
,则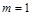 ,
,所以所求直线
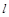 的方程为
的方程为
故正确答案为A
 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
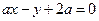 与圆
与圆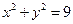 的位置关系是( )
的位置关系是( )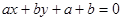 与圆
与圆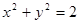 的位置关系为( )
的位置关系为( )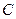 :
: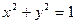 和
和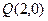 ,动点
,动点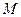 到圆
到圆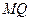 |的比等于常数
|的比等于常数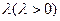 ,求动点
,求动点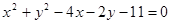 上到直线l :
上到直线l :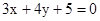 的距离等于1的点的个数是
的距离等于1的点的个数是 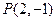 为圆
为圆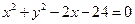 的弦
的弦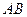 的中点,则弦
的中点,则弦 作直线
作直线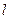 与圆
与圆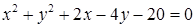 交于M、N两点,若
交于M、N两点,若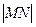 =8,则
=8,则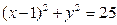 的弦AB的中点为P (2,—1),则直线AB的方程是____________________
的弦AB的中点为P (2,—1),则直线AB的方程是____________________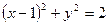 的位置关系是( )
的位置关系是( )