题目内容
已知F1、F2为双曲线C:
-
=1的左、右焦点,P在双曲线上,且PF2=5,则cos∠PF1F2______.
| x2 |
| 16 |
| y2 |
| 20 |
由F1、F2为双曲线C:
-
=1的左、右焦点,P在双曲线上,
则||PF1|-|PF2||=2a=8,
又由PF2=5,可得PF1=13,
在△F1PF2中,F1F2=2
=12,
可得△F1PF2为直角三角形,
故cos∠PF1F2=
=
.
故答案为:=
.
| x2 |
| 16 |
| y2 |
| 20 |
则||PF1|-|PF2||=2a=8,
又由PF2=5,可得PF1=13,
在△F1PF2中,F1F2=2
| 16+20 |
可得△F1PF2为直角三角形,
故cos∠PF1F2=
| F1F2 |
| F1P |
| 12 |
| 13 |
故答案为:=
| 12 |
| 13 |

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
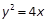 上的一点,F为抛物线的焦点,A在圆C:
上的一点,F为抛物线的焦点,A在圆C: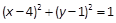 上,则
上,则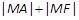 的最小值为__________.
的最小值为__________.