题目内容
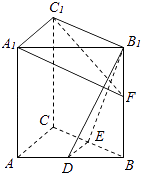
【题目】圆锥的轴截面SAB是边长为4的正三角形(S为顶点),O为底面中心,M为SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P形成的轨迹长度为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:过M作MP3⊥AM交AB于P3 , 过P3作P1P2⊥AB交圆锥底面圆周为P1 , P2 ,
则P1P2⊥平面AMP3 , ∴AM⊥P2P1 , 即P点轨迹为线段P1P2 .
∵△SAB是边长为4的等边三角形,∴AO=2,SO=2 ![]() ,∴OM=
,∴OM= ![]() =
= ![]() .
.
∵∠AMP3=90°,∴OM2=AOOP3 , 解得OP3= ![]() .
.
∴P1P2=2 ![]() =
= ![]() .
.
故选:D.
【考点精析】根据题目的已知条件,利用旋转体(圆柱、圆锥、圆台)的相关知识可以得到问题的答案,需要掌握常见的旋转体有:圆柱、圆锥、圆台、球.

练习册系列答案
相关题目
【题目】某校从参加高三期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及样本频率分布表如下:
分组 | 频数 | 频率 |
[40,50) | 2 | 0.04 |
[50,60) | 3 | 0.06 |
[60,70) | 14 | 0.28 |
[70,80) | 15 | ② |
[80,90) | ① | 0.24 |
[90,100] | 4 | 0.08 |
合计 | ③ | ④ |
(1)请把给出的样本频率分布表中的空格都填上;
(2)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[40,50)中的某一位同学,已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.