题目内容
【题目】设不等式组 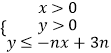 所表示的平面区域为Dn , 记Dn内的格点(格点即横坐标和纵坐标皆为整数的点)的个数为f(n)(n∈N*).
所表示的平面区域为Dn , 记Dn内的格点(格点即横坐标和纵坐标皆为整数的点)的个数为f(n)(n∈N*).
(1)求f(1)、f(2)的值及f(n)的表达式;
(2)设bn=2nf(n),Sn为{bn}的前n项和,求Sn;
(3)记 ![]() ,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
【答案】
(1)解:画出 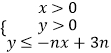 的可行域
的可行域

f(1)=2+1=3
f(2)=3+2+1=6
当x=1时,y=2n,可取格点2n个;当x=2时,y=n,可取格点n个
∴f(n)=3n
(2)解:由题意知:bn=3n2n
Sn=321+622+923+…+3(n﹣1)2n﹣1+3n2n
∴2Sn=322+623+…+3(n﹣1)2n+3n2n+1
∴﹣Sn=321+322+323+…32n﹣3n2n+1
=3(2+22+…+2n)﹣3n2n+1
=3 ![]()
=3(2n+1﹣2)﹣3nn+1
∴﹣Sn=(3﹣3n)2n+1﹣6
Sn=6+(3n﹣3)2n+1
(3)解: ![]()

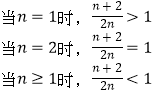
∴T1<T2=T3>T4>…>Tn
故Tn的最大值是T2=T3= ![]()
∴m≥ ![]() .
.
【解析】(1)据可行域,求出当x=1,x=2时,可行域中的整数点,分别求出f(1),f(2),f(n).(2)由于数列的通项是一个等差数列与一个等比数列的积构成的新数列,利用错位相减的方法求出数列的和.(3)求出 ![]() ,据它的符号判断出Tn的单调性,求出Tn的最大值,令m大于等于最大值即可.
,据它的符号判断出Tn的单调性,求出Tn的最大值,令m大于等于最大值即可.
【考点精析】解答此题的关键在于理解二元一次不等式(组)所表示的平面区域的相关知识,掌握不等式组表示的平面区域是各个不等式所表示的平面区域的公共部.

练习册系列答案
相关题目