题目内容
1. 如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点S,且DS=2SB,P为AC的中点.
如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点S,且DS=2SB,P为AC的中点.求证:(Ⅰ)∠PBD=30°;
(Ⅱ)AD=DC.
分析 (Ⅰ)A,B,C,D四点共圆,AC为直径,P为该圆的圆心,作PM⊥BD于点M,知M为BD的中点,即可证明∠PBD=30°;
(Ⅱ)作SN⊥BP于点N,则$SN=\frac{1}{2}SB$,证明Rt△PMS≌Rt△PNS,∠DAC=45°=∠DCA,即可证明AD=DC.
解答 证明:(Ⅰ)由已知得∠ADC=90°,从而A,B,C,D四点共圆,AC为直径,P为该圆的圆心.
作PM⊥BD于点M,知M为BD的中点,
所以∠BPM=$\frac{1}{2}∠BPD$=∠A=60°,
从而∠PBM=30°. …(5分)
(Ⅱ)作SN⊥BP于点N,则$SN=\frac{1}{2}SB$.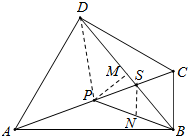
又$DS=2SB,DM=MB=\frac{1}{2}BD$,
∴$MS=DS-DM=2SB-\frac{3}{2}SB=\frac{1}{2}SB=SN$,
∴Rt△PMS≌Rt△PNS,
∴∠MPS=∠NPS=30°,
又PA=PB,所以$∠PAB=\frac{1}{2}∠NPS=15°$,
故∠DAC=45°=∠DCA,所以AD=DC.…(10分)
点评 本题考查圆的性质,考查三角形相似的证明与运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0),F1,F2分别为其左、右焦点,若其右支上存在点P满足$\frac{{|{\overrightarrow{P{F_1}}}|}}{{|{\overrightarrow{P{F_2}}}|}}$=e(e为双曲线C的离心率),则e的最大值为( )
| A. | 4$\sqrt{2}$ | B. | 3+$\sqrt{5}$ | C. | 2$\sqrt{2}$+1 | D. | 3+2$\sqrt{2}$ |
6.已知方程$\sqrt{9-{x}^{2}}$=k(x-3)+4有两个不同的实数根,则实数k的取值范围是( )
| A. | ($\frac{7}{24}$,$\frac{2}{3}$] | B. | [$\frac{2}{3}$,+∞) | C. | ($\frac{1}{3}$,$\frac{2}{3}$] | D. | (0,$\frac{7}{24}$) |
13.已知复数z=$\frac{2}{1-i}$+i(i是虚数单位),则|z|=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |