题目内容
【题目】二手车经销商小王对其所经营的![]() 型号二手汽车的使用年数
型号二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下数据:
(单位:万元/辆)进行整理,得到如下数据:
使用年数 | 2 | 3 | 4 | 5 | 6 | 7 |
售价 | 20 | 12 | 8 | 6.4 | 4.4 | 3 |
| 3.00 | 2.48 | 2.08 | 1.86 | 1.48 | 1.10 |
下面是![]() 关于
关于![]() 的散点图:
的散点图:

(I)由散点图看出,可以用线性回归模型拟合![]() 和
和![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(II)求![]() 关于
关于![]() 的回归方程,并预测某辆
的回归方程,并预测某辆![]() 型号二手汽车当使用年数为9年时,售价大约为多少?(
型号二手汽车当使用年数为9年时,售价大约为多少?(![]() 、
、![]() 的值精确到
的值精确到![]() )
)
(III)基于成本的考虑,该型号二手汽车的售价不得低于7118元,请根据(II)求出的回归方程预测在收购该型号二手汽车时,车辆的使用年数不得超过多少年?
参考公式: ,相关系数
,相关系数 .
.
参考数据:![]() ,
, ,
, ,
, ,
,![]() ,
,![]() .
.
【答案】见解析
【解析】(I)由表中数据可知,![]() ,
,![]() ,
, ![]() ,由相关系数公式可知
,由相关系数公式可知![]() 和
和![]() 的相关系数
的相关系数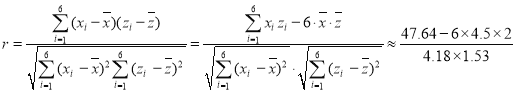
![]() .
.
从而可知![]() 和
和![]() 的线性相关程度很高.………………4分
的线性相关程度很高.………………4分
(II)由(I)及表中数据可知,![]() ,
,![]() ,
,![]() ,
,
则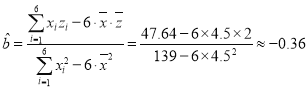 ,
,
![]() ,………………6分
,………………6分
所以![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,即
,即![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,由参考数据可知
,由参考数据可知![]() (万元).
(万元).
由此预测某辆![]() 型号二手汽车当使用年数为9年时,售价大约为1.46万元.………………8分
型号二手汽车当使用年数为9年时,售价大约为1.46万元.………………8分
(III)若该型号二手汽车的售价不得低于7118元,即![]() ,
,
则![]() ,即
,即![]() ,(10分)
,(10分)
由(II)可得![]() ,解得
,解得![]() ,
,
所以在收购该型号二手汽车时,车辆的使用年数不得超过11年.………………12分
【命题意图】本题主要考查散点图、回归直线方程,意在考查学生的识图能力、数据处理能力、运算求解能力.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目

