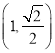题目内容
【题目】如图，已知离心率为
的椭圆
：
经过点
，且
是顶点均不与椭圆四个顶点重合的椭圆一个内接四边形．
（Ⅰ）求椭圆
的方程；
（Ⅱ）若
，试判断
的面积是否为定值？若为定值，求出该定值；若不为定值，请说明理由．
【答案】见解析
【解析】（Ⅰ）因为椭圆
的离心率为
，且过点
，
所以
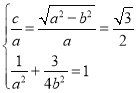，解得
，
所以椭圆
的方程为
．…………………4分
（Ⅱ）设直线
的方程为
，
，
，
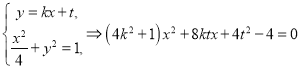，则
由根与系数的关系，得
，
，…………………6分
，
，
∴
，…………………8分
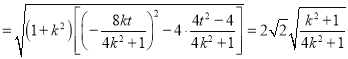．…………………9分
又∵原点
到直线的的距离为
，
∴
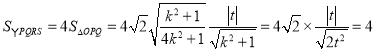，…………………11分
∴
的面积为定值，且定值为4．…………………12分
【命题意图】本题主要考查椭圆方程与几何性质、直线与椭圆的位置关系，意在考查逻辑推理能力、探索能力、运算求解能力．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
