题目内容
3.设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是( )| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(-1,0) | D. | (0,1)∪(1,+∞) |
分析 由已知当x>0时总有xf′(x)-f(x)<0成立,可判断函数g(x)=$\frac{f(x)}{x}$为减函数,由已知f(x)是定义在R上的奇函数,可证明g(x)为(-∞,0)∪(0,+∞)上的偶函数,根据函数g(x)在(0,+∞)上的单调性和奇偶性,模拟g(x)的图象,而不等式f(x)>0等价于x•g(x)>0,数形结合解不等式组即可.
解答 解:设g(x)=$\frac{f(x)}{x}$,则g(x)的导数为:g′(x)=$\frac{xf′(x)-f(x)}{{x}^{2}}$,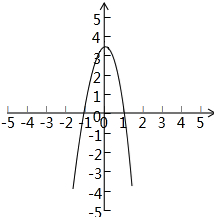
∵当x>0时总有xf′(x)<f(x)成立,
即当x>0时,g′(x)恒小于0,
∴当x>0时,函数g(x)=$\frac{f(x)}{x}$为减函数,
又∵g(-x)=$\frac{f(-x)}{-x}$=$\frac{-f(x)}{-x}$=$\frac{f(x)}{x}$=g(x),
∴函数g(x)为定义域上的偶函数
又∵g(-1)=$\frac{f(-1)}{-1}$=0,
∴函数g(x)的图象性质类似如图:
数形结合可得,不等式f(x)>0?x•g(x)>0
?$\left\{\begin{array}{l}{x>0}\\{g(x)>0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{g(x)<0}\end{array}\right.$,
?0<x<1或x<-1.
故选:A.
点评 本题主要考查了利用导数判断函数的单调性,并由函数的奇偶性和单调性解不等式,属于综合题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
14.若集合M={-1,1},N={-2,1,0}则M∩N=( )
| A. | {0.-1} | B. | {0} | C. | {1} | D. | {-1,1} |
8.设p:x<3,q:-1<x<3,则p是q成立的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
15.设A、B是两个集合,则“A∩B=A”是“A⊆B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方程是( )
| A. | 2x+y+5=0或2x+y-5=0 | B. | 2x+y+$\sqrt{5}$=0或2x+y-$\sqrt{5}$=0 | ||
| C. | 2x-y+5=0或2x-y-5=0 | D. | 2x-y+$\sqrt{5}$=0或2x-y-$\sqrt{5}$=0 |
13.函数f(x)的定义域为D,对给定的正数k,若存在闭区间[a,b]⊆D,使得函数f(x)满足:①f(x)在[a,b]内是单调函数;②f(x)在[a,b]上的值域为[ka,kb],则称区间[a,b]为y=f(x)的k级“理想区间”.下列结论错误的是( )
| A. | 函数f(x)=-x2(x∈R)存在1级“理想区间” | |
| B. | 函数f(x)=ex(x∈R)不存在2级“理想区间” | |
| C. | 函数f(x)=$\frac{4x}{{x}^{2}+1}$(x≥0)存在3级“理想区间” | |
| D. | 函数f(x)=loga(ax-$\frac{1}{4}$)(a>0,a≠1)不存在4级“理想区间” |