题目内容
18.已知ω>0,在函数y=2sinωx与y=2cosωx的图象的交点中,距离最短的两个交点的距离为2$\sqrt{3}$,则ω=$\frac{π}{2}$.分析 根据正弦线,余弦线得出交点($\frac{1}{ω}$(k1$π+\frac{π}{4}$,$\sqrt{2}$),($\frac{1}{ω}$(k2$π+\frac{5π}{4}$,$-\sqrt{2}$),k1,k2都为整数,
两个交点在同一个周期内,距离最近,即可得出方程求解即可.
解答 解:∵函数y=2sinωx与y=2cosωx的图象的交点,
∴根据三角函数线可得出交点($\frac{1}{ω}$(k1$π+\frac{π}{4}$,$\sqrt{2}$),($\frac{1}{ω}$(k2$π+\frac{5π}{4}$,$-\sqrt{2}$),k1,k2都为整数,
∵距离最短的两个交点的距离为2$\sqrt{3}$,
∴这两个交点在同一个周期内,
∴12=$\frac{1}{{ω}^{2}}$($\frac{5π}{4}$$-\frac{π}{4}$)2+($-\sqrt{2}-\sqrt{2}$)2,ω=$\frac{π}{2}$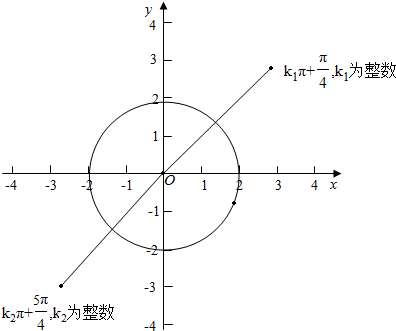
故答案为:$\frac{π}{2}$
点评 本题考查了三角函数的图象和性质,三角函数线的运用,属于中档题,计算较麻烦.

练习册系列答案
相关题目
8.若函数f(x)=$\frac{{2}^{x}+1}{{2}^{x}-a}$是奇函数,则使f(x)>3成立的x的取值范围为( )
| A. | (-∞,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,+∞) |
9.设α,β是两个不同的平面,m是直线且m?α,“m∥β“是“α∥β”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
6.设$\overrightarrow{a}$,$\overrightarrow{b}$是非零向量,“$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|”是“$\overrightarrow{a}$$∥\overrightarrow{b}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
13.设x∈R,则“x>1“是“x3>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是( )
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(-1,0) | D. | (0,1)∪(1,+∞) |
10.下列双曲线中,渐近线方程为y=±2x的是( )
| A. | x2-$\frac{y^2}{4}$=1 | B. | $\frac{x^2}{4}$-y2=1 | C. | x2-$\frac{y^2}{2}$=1 | D. | $\frac{x^2}{2}$-y2=1 |
 如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F,证明:
如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F,证明: