若变量x.y满足约束条件$\left\{\begin{array}{l}{x+y≤4}\\{x-y≤2}\\{x≥0.y≥0}\end{array}\right.$.则点的最小距离为( )A．3B．$\sqrt{17}$C．$\frac{3\sqrt{2}}{2}$D．$\frac{2\sqrt{3}}{3}$ 题目和参考答案——青夏教育精英家教网——

题目内容

1．若变量x，y满足约束条件$\left\{\begin{array}{l}{x+y≤4}\\{x-y≤2}\\{x≥0，y≥0}\end{array}\right.$，则点（3，4）到点（x，y）的最小距离为（　　）

A．

3

B．

$\sqrt{17}$

C．

$\frac{3\sqrt{2}}{2}$

D．

$\frac{2\sqrt{3}}{3}$

分析由约束条件作出可行域，再由点到直线的距离公式求得点（3，4）到点（x，y）的最小距离．

解答解：由约束条件$\left\{\begin{array}{l}{x+y≤4}\\{x-y≤2}\\{x≥0，y≥0}\end{array}\right.$作出可行域如图，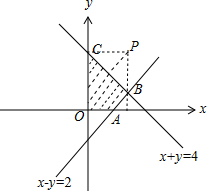

点（3，4）到点（x，y）的最小距离为P（3，4）到直线x+y-4=0的距离．
为$\frac{|3×1+4×1-4|}{\sqrt{2}}=\frac{3\sqrt{2}}{2}$．
故选：C．

点评本题考查了简单的线性规划，考查了数形结合的解题思想方法，训练了点到直线的距离公式的应用，是中档题．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

11．对于⊙A：x²+y²-2x=0，以点（$\frac{1}{2}$，$\frac{1}{2}$）为中点的弦所在的直线方程是x-y=0．

12．若{a_n}是一个各项都为正数的无穷递增等比数列，a₁和a₃是方程x²-5x+4=0的两个根，求此数列的通项公式a_n与前n项和S_n．

9．设函数f（x）=lnx，h（x）=f（x）+mf′（x）．
（1）求函数h（x）单调区间；
（2）当m=e（e为自然对数的底数）时，若h（n）-h（x）＜$\frac{e}{n}$对?x＞0恒成立，求实数n的取值范围．

16．设集合A={x||x|≤2}，B={y|y=2^x，x∈R}，则A∩B=（　　）

6．在平面直角坐标系xOy中，已知曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosα}\\{y=\sqrt{5}sinα}\end{array}\right.$（α为参数），以直角坐标系原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标轴方程为ρcos（θ-$\frac{π}{4}$）=2$\sqrt{2}$．
（1）求曲线C的普通方程与直线l的直角坐标方程；
（2）设点P为曲线C上的动点，求点P到直线l距离的最大值及其对应的点P的直角坐标．

13．直角三角形ABC中，A为直角，AB=1，BC=2，若点AM是BC边上的高线，点P在△ABC 内部或边界上运动，则$\overrightarrow{AM}$•$\overrightarrow{BP}$的范围是（　　）

[-$\frac{\sqrt{3}}{2}$，0]

[-$\frac{3}{4}$，0]

[-$\frac{\sqrt{3}}{4}$，0]

10．设不等式组$\left\{\begin{array}{l}{x+y-3≥0}\\{2x-y≥0}\\{x-2≤0}\end{array}\right.$，表示的平面区域为D，若直线mx+y+m=0上存在区域D上的点，则实数m的取值范围是$-\frac{4}{3}≤m≤-\frac{1}{3}$．

11．已知直线y=kx+2与圆（x+2）²+（y-1）²=4相交于M，N两点，若|MN|≥2$\sqrt{3}$，则k的取值范围是（　　）

[$\frac{1}{2}$，$\frac{4}{3}$]

[0，$\frac{1}{2}$]

（-∞，0]∪[$\frac{4}{3}$，+∞）

[0，$\frac{4}{3}$]