题目内容
9.设函数f(x)=lnx,h(x)=f(x)+mf′(x).(1)求函数h(x)单调区间;
(2)当m=e(e为自然对数的底数)时,若h(n)-h(x)<$\frac{e}{n}$对?x>0恒成立,求实数n的取值范围.
分析 (1)由题意先求函数h(x)的定义域,再求导h′(x),从而讨论导数的正负以确定函数的单调性;
(2)由h(n)-h(x)<$\frac{e}{n}$转化为$lnn<lnx+\frac{e}{x}$,即$lnn<(lnx+\frac{e}{x})_{min}$成立,利用导数求出
$g(x)=lnx+\frac{e}{x}$在(0,e)上的最小值即可.
解答 解:(1)${f}^{′}(x)=\frac{1}{x}$,
h(x)=$lnx+\frac{m}{x}$,定义域为(0,+∞)
${h}^{′}(x)=\frac{1}{x}-\frac{m}{{x}^{2}}$=$\frac{x-m}{{x}^{2}}$
当m≤0时,在(0,+∞)上h′(x)>0,此时h(x)在(0,+∞)单调递增,
当m>0时,在(0,m)上h′(x)<0,此时h(x)在(0,m)单调递减,
在(m,+∞)上h′(x)>0,h(x)在(m,+∞)上单调递增,
综上:当m≤0时,h(x)在(0,+∞)单调递增,
当m>0时,h(x)在(0,m)单调递减,在(m,+∞)上单调递增;
(2)当m=e时,$h(x)=lnx+\frac{e}{x}$,不等式为$lnn+\frac{e}{n}-lnx-\frac{e}{x}<\frac{e}{n}$
即$lnn<lnx+\frac{e}{x}$
只需$lnn<(lnx+\frac{e}{x})_{min}$
由(1)知,$g(x)=lnx+\frac{e}{x}$在(0,e)上单调递减,在(e,+∞)上单调递增,
∴当x=m时,gmin(x)=g(e)=2
故lnn<2,可得0<n<e2
∴n的取值范围为(0,e2).
点评 本题考查了,利用导数求函数的单调区间,运用了等价转换等数学思想,是一道导数的综合题,难度中等.

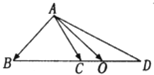 在△ABC中,点D在线段BC的延长线上,且$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围是( )
在△ABC中,点D在线段BC的延长线上,且$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围是( )| A. | (-1,0) | B. | (0,$\frac{1}{3}$) | C. | (0,1) | D. | (-$\frac{1}{3}$,0) |
| A. | $\frac{1}{2}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
| A. | 3 | B. | $\sqrt{17}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
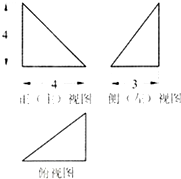 某四面体的三视图如图所示,该四面体的体积是8,该四面体四个面的面积中最大的是10.
某四面体的三视图如图所示,该四面体的体积是8,该四面体四个面的面积中最大的是10.