题目内容
16．设集合A={x||x|≤2}，B={y|y=2x，x∈R}，则A∩B=（ ）| A． | （0，2] | B． | [-2，2） | C． | [0，2） | D． | [2，+∞） |
分析 根据题意，解|x|≤2可得集合，B为函数y=2x的值域，由指数函数的性质可得集合B，进而由交集的意义，计算可得答案．
解答 解：根据题意，集合B={y|y＞0}=（0，+∞），
集合A={x||x|≤2=[-2，2]，
则A∩B=（0，2]；
故选：A．
点评 本题考查集合的交集的运算，关键是由集合的意义正确求出集合A、B．
练习册系列答案
相关题目
4．
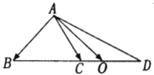在△ABC中，点D在线段BC的延长线上，且$\overrightarrow{BC}$=$\overrightarrow{CD}$，点O在线段CD上（点O与点C，D不重合），若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$，则x的取值范围是（ ）
在△ABC中，点D在线段BC的延长线上，且$\overrightarrow{BC}$=$\overrightarrow{CD}$，点O在线段CD上（点O与点C，D不重合），若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$，则x的取值范围是（ ）| A． | （-1，0） | B． | （0，$\frac{1}{3}$） | C． | （0，1） | D． | （-$\frac{1}{3}$，0） |
11．在△ABC中，内角A，B，C所对应的边分别为a，b，c，若bsinA-$\sqrt{3}$acosB=0，且b2=ac，则$\frac{b}{a+c}$的值为
（ ）
（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\sqrt{2}$ | C． | 2 | D． | $\frac{1}{2}$ |
1．若变量x，y满足约束条件$\left\{\begin{array}{l}{x+y≤4}\\{x-y≤2}\\{x≥0，y≥0}\end{array}\right.$，则点（3，4）到点（x，y）的最小距离为（ ）
| A． | 3 | B． | $\sqrt{17}$ | C． | $\frac{3\sqrt{2}}{2}$ | D． | $\frac{2\sqrt{3}}{3}$ |
在△ABC中，三个内角A，B，C的对边分别为a，b，c，其中c=2，且$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\frac{\sqrt{3}}{1}$．
5．设f（x）为定义在R上的奇函数，且是周期为4的周期函数，f（1）=1，则f（-1）+f（8）=（ ）
| A． | -2 | B． | -1 | C． | 0 | D． | 1 |