题目内容
【题目】函数![]() 和
和![]() 都是定义在
都是定义在![]() 上的单调减函数,且
上的单调减函数,且![]() ,若对于任意
,若对于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 在
在![]() 上的“被追逐函数”,若
上的“被追逐函数”,若![]() ,下述四个结论中正确的是( )
,下述四个结论中正确的是( )
①![]() 是
是![]() 在
在![]() 上的“被追逐函数”;
上的“被追逐函数”;
②若![]() 和函数
和函数![]() 关于
关于![]() 轴对称,则
轴对称,则![]() 是
是![]() 在
在![]() 上的“被追逐函数”;
上的“被追逐函数”;
③若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,则
上的“被追逐函数”,则![]() ;
;
④存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“被追逐函数”.
上的“被追逐函数”.
A.①③④B.①②④C.②③D.①③
【答案】D
【解析】
先判断![]() 与
与![]() 是否单调递减,并求得最小值,再根据若
是否单调递减,并求得最小值,再根据若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,
上的“被追逐函数”,![]() ,则
,则![]() 可用
可用![]() 表示,利用
表示,利用![]() ,代入判断其是否恒成立,即可判断是否满足“被追逐函数”,由此依次判断①②③④
,代入判断其是否恒成立,即可判断是否满足“被追逐函数”,由此依次判断①②③④
对于①,![]() 和
和![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,
若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,则对于任意
上的“被追逐函数”,则对于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,即
成立,即![]() ,所以
,所以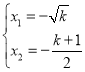 ,
,
此时![]() ,即
,即![]() ,构造函数
,构造函数![]() ,则
,则![]() ,则
,则![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,则
,则![]() 恒成立,即
恒成立,即![]() ,故对任意
,故对任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,故①正确;
成立,故①正确;
对于②,依题意![]() ,则
,则![]() 和
和![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,若
,若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,则对于任意
上的“被追逐函数”,则对于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,即
成立,即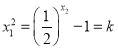 ,所以
,所以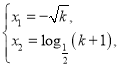 当
当![]() 时,不存在
时,不存在![]() ,
,![]() ,使得
,使得![]() 成立,故②错误;
成立,故②错误;
对于③,若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,此时必有
上的“被追逐函数”,此时必有![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() 和
和![]() 在
在![]() 上单调递减,若
上单调递减,若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,则对于任意
上的“被追逐函数”,则对于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,即
成立,即![]() ,所以
,所以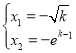 ,即
,即![]() ,则
,则![]() ,构造函数
,构造函数![]() ,则
,则![]() ,则
,则![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,则
,则![]() 恒成立,即
恒成立,即![]() ,故对任意
,故对任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,故③正确;
成立,故③正确;
对于④,当![]() 时,
时,![]() ,而当
,而当![]() 时,
时,![]() ,由
,由![]() 的任意性,不存在
的任意性,不存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“被追逐函数”,故④错误,
上的“被追逐函数”,故④错误,
故选:D

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目