Question

【题目】棱长为的正四面体的外接球与内切球的半径之和为______，内切球球面上有一动点，则的最小值为______.

Answer 1

【答案】

【解析】

(1)将正四面体放入正方体可求得外接球半径,利用等体积法可求得内切球的半径.

(2)根据阿波罗尼斯球的性质找到阿波罗尼斯球中的两个定点,再将转换,从而得出取最小值时的线段,再根据余弦定理求解即可.

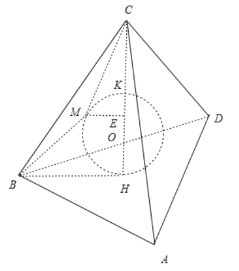
(1) 将正四面体放入如图正方体,则正四面体的外接球与该正方体的外接球为同一球.半径为.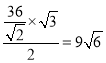

设正四面体的内切球半径为,根据等体积法有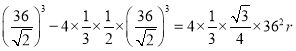,解得.

故外接球与内切球的半径之和为.

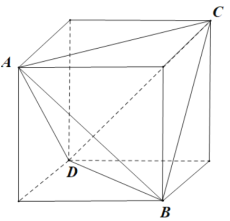
(2)由阿波罗尼斯球得内切球球心是线段上以为定点,空间中满足的点的集合,连接并延长交平面于,交内切球上方的点设为,过作,交于,连接,设.

由(1)空得.

所以,解得,,

所以,所以.

所以,

在中,,,,

所以.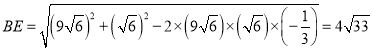

所以的最小值为

故答案为：(1)；(2)