题目内容
【题目】设椭圆![]() 的离心率
的离心率![]() ,左焦点为
,左焦点为![]() ,右顶点为
,右顶点为![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,若直线
两点,若直线![]() 垂直于
垂直于![]() 轴时,有
轴时,有![]() .
.
(1)求椭圆的方程;
(2)设直线![]() :
: ![]() 上两点
上两点![]() ,
, ![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与椭圆相交于点
与椭圆相交于点![]() (
(![]() 异于点
异于点![]() ),直线
),直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)由离心率可得![]() 的关系,再由
的关系,再由![]() ,结合隐含条件,求得
,结合隐含条件,求得![]() 的值,即可得到椭圆的方程;
的值,即可得到椭圆的方程;
(2)设直线![]() 的方程为
的方程为![]() ,与直线
,与直线![]() 的方程联立,可得点
的方程联立,可得点![]() 的坐标,进一步得到
的坐标,进一步得到![]() 的坐标,联立直线与椭圆的方程,求得
的坐标,联立直线与椭圆的方程,求得![]() 的坐标,则
的坐标,则![]() 所在的直线方程可求,取
所在的直线方程可求,取![]() ,求得
,求得![]() 的坐标,得到
的坐标,得到![]() ,结合
,结合![]() 的面积为
的面积为![]() ,即可求解实数
,即可求解实数![]() 的值,得到直线方程.
的值,得到直线方程.
试题解析:
(1)设![]() ,因为
,因为![]() 所以有
所以有![]() ,又由
,又由![]() 得
得![]() ,
,
且![]() ,得
,得![]() ,因此椭圆的方程为:
,因此椭圆的方程为: ![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,与直线
,与直线![]() 的方程
的方程![]() 联立,可得点
联立,可得点![]() ,故
,故![]() .将
.将![]() 与
与![]() 联立,消去
联立,消去![]() ,整理
,整理![]() , 解得
, 解得![]() ,或
,或![]() .由点
.由点![]() 异于点
异于点![]() ,
,
可得点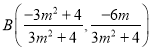 .由
.由![]() ,可得直线
,可得直线![]() 的方程为
的方程为
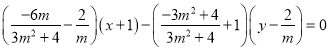 ,令
,令![]() ,
,
解得![]() ,故
,故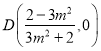 . 所以
. 所以![]() .
.
又因为![]() 的面积为
的面积为![]() ,故
,故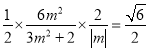 ,
,
整理得![]() ,解得
,解得![]() .
.
所以,直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】某种设备随着使用年限的增加,每年的维护费相应增加![]() 现对一批该设备进行调查,得到这批设备自购入使用之日起,前五年平均每台设备每年的维护费用大致如表:
现对一批该设备进行调查,得到这批设备自购入使用之日起,前五年平均每台设备每年的维护费用大致如表:
年份 | 1 | 2 | 3 | 4 | 5 |
维护费 |
|
|
|
|
|
![]() Ⅰ
Ⅰ![]() 求y关于t的线性回归方程;
求y关于t的线性回归方程;
![]() Ⅱ
Ⅱ![]() 若该设备的价格是每台5万元,甲认为应该使用满五年换一次设备,而乙则认为应该使用满十年换一次设备,你认为甲和乙谁更有道理?并说明理由.
若该设备的价格是每台5万元,甲认为应该使用满五年换一次设备,而乙则认为应该使用满十年换一次设备,你认为甲和乙谁更有道理?并说明理由.
![]() 参考公式:
参考公式: ,
,![]()