��Ŀ����
����Ŀ��Ϊ�˵���ij����ӻ����������о���Ա�Ըÿ���ӻ���������Ӧ�IJ��ԣ����õ������ݷ��飺![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����ͳ����ͼ��ʾ��
����ͳ����ͼ��ʾ��
���Բ�ͬ�Ա������������ӻ��Ĺ�����Ը�������飬�õ����������±���ʾ��
Ը���ÿ���ӻ� | ��Ը���ÿ���ӻ� | �ܼ� | |
���� | 800 | 1000 | |
�� | 600 | ||
�ܼ� | 1200 |
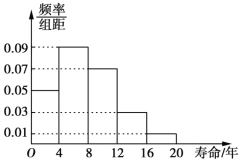
��1������ͼ�е����ݣ��Թ��Ƹÿ���ӻ���ƽ��������
��2�����ݱ������ݣ��ܷ��ڷ�����ĸ��ʲ�����0.001��ǰ������Ϊ���Ƿ�Ը���ÿ���ӻ����롰������Ա��йأ�
��3����Ƶ�ʹ��Ƹ��ʣ����ڸÿ���ӻ����������������ȡ4̨������������������4��ĵ��ӻ���̨��ΪX����X�ķֲ��м���ѧ����.
�ο���ʽ�����ݣ�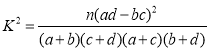 ������
������![]() ��
��
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
���𰸡���1���ÿ���ӻ���ƽ������ԼΪ7.76�ꣻ ��2���ڷ�����ĸ��ʲ�����0.001��ǰ������Ϊ���Ƿ�Ը���ÿ���ӻ�������������Ա����й�.�� ��3��![]() .
.
��������
��1������Ƶ�ʷֲ�ֱ��ͼ����������ݵ�Ƶ�ʣ����ø����Ƶ�ʳ��Ը������ݵ��м�ֵ����ͼ��õ�ƽ������
��2�������Ʊ������ݣ��ɱ������ݼ���![]() �Ĺ۲�ֵ���ٽ����жϡ�
�Ĺ۲�ֵ���ٽ����жϡ�
��3����Ƶ�ʷֲ�ֱ��ͼ��֪���ӻ���������������ĸ���Ϊ![]() ���г��ֲ�������������
���г��ֲ�������������
��1��![]()
![]() ��
��
�ʸÿ���ӻ���ƽ������ԼΪ7.76��.
��2�������⣬���Ʊ��е��������±���ʾ��
Ը���ÿ���ӻ� | ��Ը���ÿ���ӻ� | �ܼ� | |
���� | 800 | 200 | 1000 |
�� | 400 | 600 | 1000 |
�ܼ� | 1200 | 800 | 2000 |
�����![]() �Ĺ۲�ֵΪ
�Ĺ۲�ֵΪ![]() .
.
�����ڷ�����ĸ��ʲ�����0.001��ǰ������Ϊ���Ƿ�Ը���ÿ���ӻ�������������Ա����й�.
��3�������⣬![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() .
.
��X�ķֲ���Ϊ
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
![]() .
.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�