题目内容
【题目】若方程![]() 有实数根
有实数根![]() ,则称
,则称![]() 为函数
为函数![]() 的一个不动点.已知函数
的一个不动点.已知函数![]() (
(![]() ).
).
(1)若![]() ,求证:
,求证:![]() 有唯一不动点;
有唯一不动点;
(2)若![]() 有两个不动点,求实数a的取值范围.
有两个不动点,求实数a的取值范围.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)依题意,令![]() (
(![]() ),利用导数可知
),利用导数可知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,且
上单调递增,且![]() 时,
时,![]() 取的最小值0,由此即可得出结论;
取的最小值0,由此即可得出结论;
(2)先证明![]() ,则
,则![]() 有两个不动点等价于函数
有两个不动点等价于函数![]() 在
在![]() 上有两个不同的零点,求出
上有两个不同的零点,求出![]() 的导数,得到其单调性,得到函数的最小值
的导数,得到其单调性,得到函数的最小值![]() ,即可得到
,即可得到![]() 的取值范围,再证明
的取值范围,再证明![]() 时,
时,![]() 有两个零点;
有两个零点;
解:(1)证明:当![]() 时,由
时,由![]() 得
得![]() ,
,
令![]() (
(![]() ),
),
则![]() ,易知
,易知![]() 在
在![]() 上恒成立,
上恒成立,
故当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
∴方程![]() 有唯一实数根
有唯一实数根![]() ,故
,故![]() 有唯一不动点;
有唯一不动点;
(2)先证明![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,从而
,从而![]() ,因此
,因此![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,所以
,所以![]() ,即
,即![]() ,
,![]() 有两个不动点等价于函数
有两个不动点等价于函数![]() 在
在![]() 上有两个不同的零点,
上有两个不同的零点,
易知![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以有
,所以有![]() ,所以
,所以![]() ,即
,即![]() ,
,
下面说明![]() 时,
时,![]() 有两个零点,取
有两个零点,取![]() 有
有![]() ,故
,故![]() ,取
,取![]() ,且
,且![]() ,故
,故![]() ,又
,又![]() ,由零点存在性定理知
,由零点存在性定理知![]() 在
在![]() 存在唯一
存在唯一![]() ,使得
,使得![]() ,在
,在![]() 内存在
内存在![]() 使
使![]() ,综上有
,综上有![]() .
.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
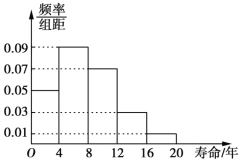
学习实践园地系列答案【题目】为了调查某款电视机的寿命,研究人员对该款电视机进行了相应的测试,将得到的数据分组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并统计如图所示:
,并统计如图所示:
并对不同性别的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
愿意购买该款电视机 | 不愿意购买该款电视机 | 总计 | |
男性 | 800 | 1000 | |
女性 | 600 | ||
总计 | 1200 |
(1)根据图中的数据,试估计该款电视机的平均寿命;
(2)根据表中数据,能否在犯错误的概率不超过0.001的前提下认为“是否愿意购买该款电视机”与“市民的性别”有关;
(3)以频率估计概率,若在该款电视机的生产线上随机抽取4台,记其中寿命不低于4年的电视机的台数为X,求X的分布列及数学期望.
参考公式及数据: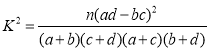 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |