题目内容
【题目】已知函数g（x）= 
是奇函数，f（x）=log4（4x+1）﹣mx是偶函数．
（1）求m+n的值；
（2）设h（x）=f（x）+ 
x，若g（x）＞h[log4（2a+1）]对任意x≥1恒成立，求实数a的取值范围．
【答案】
（1）解：由于g（x）为奇函数，且定义域为R，
∴g（0）=0，即 
=0，∴n=﹣1，
∵f（x）=log4（4x+1）﹣mx
∴f（﹣x）=log4（4x+1）﹣（﹣m+1）x，
∵f（x）是偶函数，
∴f（﹣x）=f（x），得﹣mx=﹣（﹣m+1）x恒成立，故m= 
，
综上所述，可得m+n=﹣
（2）解：∵h（x）=f（x）+ x=log4（4x+1），
∴h[log4（2a+1）]=log4（2a+2），
又∵g（x）=2x﹣2﹣x在区间[1，+∞）上是增函数，
∴当x≥1时，g（x）min= 
由题意，得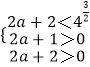 
，∴ 
因此，实数a的取值范围是：{a|﹣ 
}
【解析】（1）由g（x）为定义在R上的奇函数，得g（0）=0，解得n=﹣1；再根据偶函数满足f（﹣x）=f（x），比较系数可得m= ，由此即可得到m+n的值．（2）由（1）得h（x）=log4（4x+1），易得h[log4（2a+1）]=log4（2a+2）．而定义在R上的增函数g（x）在x≥1时的最小值为g（1）= ，从而不等式转化成 ＞log4（2a+2），由此再结合真数必须大于0，不难解出实数a的取值范围．
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点，需要掌握在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇才能正确解答此题．
