Question

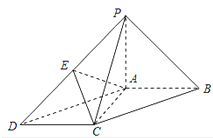
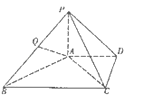
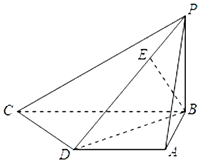
【题目】如图四边形ABCD，AB=BD=DA=2．BC=CD= ，现将△ABD沿BD折起，使二面角A﹣BD﹣C的大小在[ ， ]，则直线AB与CD所成角的余弦值取值范围是（ ）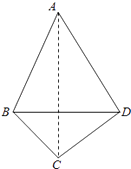
A.[0， ]∪（ ，1）
B.[ ， ]
C.[0， ]
D.[0， ]

Answer 1

【答案】D
【解析】解：取BD中点O，连结AO，CO， ∵AB=BD=DA=2．BC=CD= ，∴CO⊥BD，AO⊥BD，且CO=1，AO= ，
∴∠AOC是二面角A﹣BD﹣C的平面角，
以O为原点，OC为x轴，OD为y轴，
过点O作平面BCD的垂线为z轴，建立空间直角坐标系，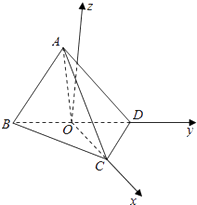

B（0，﹣1，0），C（1，0，0），D（0，1，0），
设二面角A﹣BD﹣C的平面角为θ，则 ，
连AO、BO，则∠AOC=θ，A（ ），
∴ ， ，
设AB、CD的夹角为α，
则cosα= = ，
∵ ，∴cos ，∴|1﹣ |∈[0， ]．
∴cos ．
故选：D．
【考点精析】本题主要考查了异面直线及其所成的角的相关知识点，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能正确解答此题．