题目内容
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,E,F是线段B1D上的两个动点,且EF= ![]() ,则下列结论错误的是( )
,则下列结论错误的是( ) 
A.AC⊥BF
B.直线AE,BF所成的角为定值
C.EF∥平面ABC
D.三棱锥A﹣BEF的体积为定值
【答案】B
【解析】解:∵在正方体中,AC⊥BD,∴AC⊥平面B1D1DB,又BE平面BB1D1D,∴AC⊥BE,故A正确; ∵当点E在D1处,F为D1B1的中点时,异面直线AE,BF所成的角是∠OEB,当E在上底面的中心时,F在C1的位置,异面直线AE,BF所成的角是∠OE1B,显然两个角不相等,B不正确;
∵平面ABCD∥平面A1B1C1D1 , EF平面A1B1C1D1 , ∴EF∥平面ABCD,故C正确;
∵由于点B到直线B1D1的距离不变,故△BEF的面积为定值.又点A到平面BEF的距离为 ![]() ,故VA﹣BEF为定值.D正确;
,故VA﹣BEF为定值.D正确;
故选B.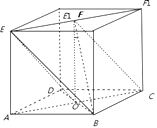
通过直线AC垂直平面平面BB1D1D,判断A是正确的;通过直线EF垂直于直线AB1 , AD1 , 判断A1C⊥平面AEF是正确的;计算三角形BEF 的面积和A到平面BEF的距离是定值,说明C是正确的;只需找出两个特殊位置,即可判断D是不正确的;综合可得答案.

练习册系列答案
相关题目