题目内容
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当![]() ,求函数
,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
【答案】(1)![]() ;(2)
;(2)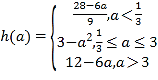 ;(3)
;(3)![]() ,
,![]()
【解析】
(1)因为![]() 的定义域为
的定义域为![]() ,所以
,所以![]() 对任意实数
对任意实数![]() 恒成立.当m=0时显然不满足,当m不为0时,内层函数为二次函数,需要开口向上且判别式小于0,即可满足要求.
恒成立.当m=0时显然不满足,当m不为0时,内层函数为二次函数,需要开口向上且判别式小于0,即可满足要求.
(2)x∈[-1,1]时,求函数![]() 是一个复合函数,复合函数的最值一般分两步来求,第一步求内层函数的值域,第二步研究外层函数在内层函数值域上的最值,本题内层函数的值域是确定的一个集合,而外层函数是一个系数有变量的二次函数,故本题是一个区间定轴动的问题.
是一个复合函数,复合函数的最值一般分两步来求,第一步求内层函数的值域,第二步研究外层函数在内层函数值域上的最值,本题内层函数的值域是确定的一个集合,而外层函数是一个系数有变量的二次函数,故本题是一个区间定轴动的问题.
(3) 根据函数的单调性,列出方程组![]() 转化为:即m、n是方程
转化为:即m、n是方程![]() 的两非负实根,且m<n.即可得解.
的两非负实根,且m<n.即可得解.
(1)由题意![]() 对任意实数
对任意实数![]() 恒成立,
恒成立,
∵![]() 时显然不满足
时显然不满足
∴![]()
∴![]()
(2)令![]() ,则
,则![]()
∴ 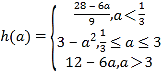
(3)∵ ![]()
∴ ![]() ∴
∴ ![]()
∴ 函数![]() 在[
在[![]() ,
,![]() ]单调递增,
]单调递增,
∴ ![]() 又∵
又∵ ![]()
∴ ![]() ,
,![]()

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
【题目】某学校900名学生在一次百米测试中,成绩全部介于13秒与18 秒之间,利用分层抽样的方法抽取其中若干个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],有关数据见下表:
各组组员数 | 各组抽取人数 | |
[13,14) | 54 | a |
[14,15) | b | 8 |
[15,16) | 342 | 19 |
[16,17) | 288 | c |
[17,18] | d |
(1)求a,b,c,d的值;
(2)若样本第一组中只有一个女生,其他都是男生,第五组则只有一个男生,其他都是女生,现从第一、五组中各抽一个同学组成一个新的组,求这个新组恰好由一个男生和一个女生构成的概率。