题目内容
【题目】在如图所示的五面体中,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]()
![]() ,
,![]() ,
, ![]() ,点
,点![]() 在
在![]() 上.
上.
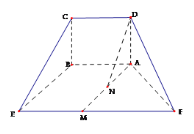
求证:(1)![]() 平面
平面![]()
(2)平面![]()
![]() 平面
平面![]()
【答案】详见解析
【解析】
(1)先证明平面![]() 平面
平面![]() ,进而由面面平行可得线面平行;
,进而由面面平行可得线面平行;
(2)利用勾股定理的逆定理证明直线![]() ,由面面垂直的性质得到
,由面面垂直的性质得到![]() 平面
平面![]() ,进而可得
,进而可得![]() 平面
平面![]() ,从而可得平面
,从而可得平面![]()
![]() 平面
平面![]() .
.
证明:(1)连结DM
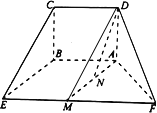
∵AB∥EF,AB=![]() EF,M是EF的中点,
EF,M是EF的中点,
∴AB∥EM且AB![]() EM,四边形ABEM是平行四边形,
EM,四边形ABEM是平行四边形,
∴AM∥BE,又∵AM平面BCE,BE平面BCE,
∴AM∥平面BCE.∵四边形ABCD是矩形,
∴AD∥BC,又BC平面BCE,AD平面BCE,∴AD∥平面BCE,
又AD平面ADM,AM平面ADM,AD∩AM=A,
∴平面ADM∥平面BCE,
又DN平面ADM,
∴DN∥平面BCE(2)由(1)知AM=BE=2,
∵AF=BE=2,MF=![]() EF=
EF=![]()
∴AM2+AF2=MF2,∴AM⊥AF.
∵平面ADF⊥平面ABEF,平面ADF∩平面ABEF=AF,AM平面ABEF,
∴AM⊥平面DAF,∵DA平面DAF,
∴AM⊥DA,
又∵四边形ABCD是矩形,∴AD⊥AB,
∵AB平面ABEF,AM平面ABEF,AB∩AM=A,
∴AD⊥平面ABEF,又AD平面ABCD,
∴平面ABEF⊥平面ABCD

练习册系列答案
相关题目