题目内容
【题目】如图，在四边形
中，
，
， 
，
，
，
是
上的点，
，
为
的中点，将
沿 折起到
的位置，使得
，如图2.
（1）求证：平面
平面
；
（2）求二面角
的余弦值.
【答案】（1）见解析;（2）
．
【解析】试题分析：(1)由四边形
为菱形，且
为等边三角形得
，结合勾股定理得
，利用判定定理证明(2) 建立空间直角坐标系
，求平面
的法向量
和平面
的法向量
，利用公式求得结果
解析：（1）连结
．
在四边形
中，
，
，
，
，
，
，
∴
，
，
四边形为菱形，且为等边三角形．
又∵
为
的中点，∴.
∵
，
，
，满足
，
∴，
又∵
，∴
平面.
∵
平面
，∴平面 
平面．
（2）以为原点，向量
的方向分别为
轴、
轴的正方向建立空间直角坐标系（如图），
则
，
，
，
所以
，
，
设
是平面的一个法向量，
则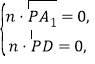
即
取
，得
．
取平面的一个法向量
．
∵
，
又二面角
的平面角为钝角，
所以二面角的余弦值为
．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
【题目】为了确保神舟飞船发射时的信息安全，信息须加密传输，发送方由明文→密文（加密），接受方由密文→明文（解密），已知加密的方法是：密码把英文的明文（真实文）按字母分解，其中英文的a，b，c，…，z的26个字母（不论大小写）依次对应1，2，3，…，26这26个自然数（见下表）：
a | b | c | d | e | f | g | h | i | j | k | l | m |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
n | o | p | q | r | s | t | u | v | w | x | y | z |
14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
通过变换公式：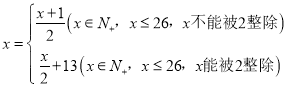
，将明文转换成密文，如
，即h变换成q；
，即e变换成c．若按上述规定，若将明文译成的密文是shxc，那么原来的明文是__________．
