Question

【题目】设集合，，若，则实数的取值范围是_____.

Answer 1

【答案】

【解析】

若A∩B≠，得x2+2（1﹣a）x+3﹣a≤0在x∈[0，3]有解，分离变量再构造函数g（t），转为求函数最值即可得解.

集合A＝{x|x2+2（1﹣a）x+3﹣a≤0}，B＝{x|0≤x≤3}，

若A∩B≠，得x2+2（1﹣a）x+3﹣a≤0在x∈[0，3]有解，

即（2x+1）a≥x2+2x+3在x∈[0，3]有解，

设t＝2x+1，则t∈[1，7]，则x＝，

则a≥＝，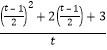

设g（t）＝，t∈[1，7]，

由对勾函数的性质可得y＝g（t）在（1，3）为减函数，在（3，7）上为增函数，又g（t）的最小值为g(3)＝2，

所以实数a的取值范围是[2，+∞），

故答案为：[2，+∞）