题目内容
【题目】已知函数f（x）是定义域在R上的奇函数，当x＞0时，f（x）=x2﹣2x．
（1）求出函数f（x）在R上的解析式；
（2）写出函数的单调区间．
【答案】（1）f（x）=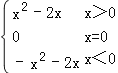
；
（2）则函数的单调递增区间为为[1，+∞），（﹣∞，﹣1]，函数的单调递减区间为为[﹣1，1]．
【解析】
试题（1）根据函数f（x）为定义域为R的奇函数，当x＞0时，f（x）=x2﹣2x，我们根据定义域为R的奇函数的图象必过原点，则f（﹣x）=﹣f（x），即可求出函数f（x）在R上的解析式；
（2）根据（1）中分段函数的解析式，我们易画出函数f（x）的图象，利用数形结合进行求解即可．
解：（1）∵函数f（x）是定义域在R上的奇函数，
∴当x=0时，f（0）=0；
当x＜0时，﹣x＞0，则f（﹣x）=x2+2x．
∵f（x）是奇函数，
∴f（﹣x）=﹣f（x）
∴f（﹣x）=x2+2x=﹣f（x），
即f（x）=﹣x2﹣2x．
综上：f（x）=．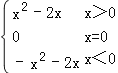
（2）函数f（x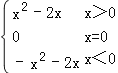）=的图象如下图所示：
则函数的单调递增区间为为[1，+∞），（﹣∞，﹣1]，
函数的单调递减区间为为[﹣1，1]．
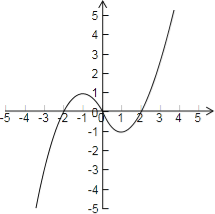
练习册系列答案
阅读快车系列答案
相关题目
