题目内容
【题目】某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元,2000元.甲、乙产品都需要在A、B两种设备上加工,在每台A、B设备上加工一件甲所需工时分别为1![]() ,2
,2![]() ,加工一件乙设备所需工时分别为2
,加工一件乙设备所需工时分别为2![]() ,1
,1![]() .A、B两种设备每月有效使用台时数分别为400
.A、B两种设备每月有效使用台时数分别为400![]() 和500
和500![]() ,分别用
,分别用![]() 表示计划每月生产甲,乙产品的件数.
表示计划每月生产甲,乙产品的件数.
(Ⅰ)用![]() 列出满足生产条件的数学关系式,并画出相应的平面区域;
列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别生产甲、乙两种产品各多少件,可使收入最大?并求出最大收入.
【答案】(1)见解析(2)安排生产甲、乙两种产品月的产量分别为200,100件可使月收入最大,最大为80万元.
【解析】试题分析:(1)设甲、乙两种产品月的产量分别为x,y件,列出约束条件和目标函数,画出可行域。(2)由可行域及目标函数,可出得最优解,注意x,需取整。
试题解析:(Ⅰ)设甲、乙两种产品月的产量分别为x,y件,
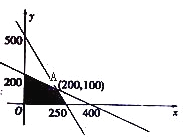
约束条件是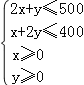 ,由约束条件画出可行域,如图所示的阴影部分
,由约束条件画出可行域,如图所示的阴影部分
(Ⅱ)设每月收入为z千元,目标函数是z=3x+2y
由z=3x+2y可得y=﹣![]() x+
x+![]() z,截距最大时z最大.
z,截距最大时z最大.
结合图象可知,z=3x+2y在A处取得最大值
由![]() 可得A(200,100),此时z=800
可得A(200,100),此时z=800
故安排生产甲、乙两种产品月的产量分别为200,100件可使月收入最大,最大为80万元.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目