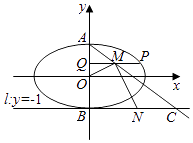题目内容
【题目】在平面直角坐标系xOy中，已知△ABC的两个顶点A，B的坐标分别为（﹣1，0），（1，0），且AC、BC所在直线的斜率之积等于﹣2，记顶点C的轨迹为曲线E．
（1）求曲线E的方程；
（2）设直线y=2x+m（m∈R且m≠0）与曲线E相交于P、Q两点，点M（ 
，1），求△MPQ面积的取值范围．
【答案】
（1）解：设C（x，y），由题意，可得 
=﹣2（x≠±1），
∴曲线E的方程为 
=1（x≠±1）
（2）解：设P（x1，y1），Q（x2，y2），
联立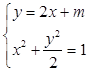 
，消去y，得6x2+4mx+m2﹣2=0，
∵△=48﹣8m2＞0，∴m2＜6，
∵x≠±1，∴m≠±2，
又∵m≠0，∴0＜m2＜6，且m2≠4，
∵ 
， 
，
∴|PQ|= 
|x1﹣x2|= 
= 
= 
．
点M（ 
，1）到PQ的距离d= 
= 
，
∵0＜m2＜6，m2≠4，
∴ 
=（ 
）2= 
= 
m2m2（12﹣2m2）
≤ （ 
）3= 
= 
，
当且仅当m2=12﹣2m2时，取等号，又m2≠4，
∴ ∈（0， 
）．
∴△MPQ面积的取值范围是（0， 
）
【解析】（1）设C（x，y），由题意，可得 
=﹣2（x≠±1），由此能求出曲线E的方程．（2）设P（x1，y1），Q（x2，y2），联立 
，得6x2+4mx+m2﹣2=0，由此利用根的判别式、韦达定理、弦长公式、三角形面积公式，结合已知条件能求出△MPQ面积的取值范围．
练习册系列答案
名校课堂系列答案
相关题目
