Question

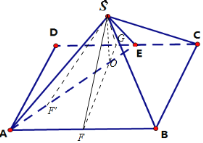
【题目】如图，点E为正方形ABCD边CD上异于点C、D的动点，将△ADE沿AE翻折成△SAE，在翻折过程中，下列三个说法中正确的个数是（ ）

①存在点E和某一翻折位置使得AE∥平面SBC；

②存在点E和某一翻折位置使得SA⊥平面SBC；

③二面角S﹣AB﹣E的平面角总是小于2∠SAE．

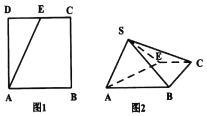
A.0B.1C.2D.3

Answer 1

【答案】B

【解析】

对于①，四边形ABCE为梯形，所以AE与BC必然相交；对于②，假设SA平面SBC，可推得矛盾；对于③，当将△ADE沿AE翻折使得平面SAE⊥平面ABCE时，二面角S﹣AB﹣E最大，在平面SAE内，作出一个角等于二面角S﹣AB﹣E的平面角；由角所在三角形的一个外角，它是不相邻的两个内角之和，结合图形，即可判定③．

对于①，四边形ABCE为梯形，所以AE与BC必然相交，故①错误；

对于②，假设SA平面SBC，SC平面SBC，所以SA⊥SC，又SA⊥SE，SE∩SC＝S，所以SA⊥平面SCE，所以平面SCE∥平面SBC，这与平面SBC∩平面SCE＝SC矛盾，

故假设不成立，即②错误；

对于③，当将△ADE沿AE翻折使得平面SAE⊥平面ABCE时，二面角S﹣AB﹣E最大，如图，在平面SAE内，作SO⊥AE，垂足为O，∴SO⊥平面ABCE；AB平面ABCE，

所以SO⊥AB；

作OF⊥AB，垂足为F，连接SF，SO∩OF＝O，则AB⊥平面SFO，所以AB⊥SF，则∠SFG即为二面角S﹣AB﹣E的平面角；

在直线AE上取一点，使得O＝OF，连接S，则∠SO＝∠SFO；

由图形知，在△SA中，S＞A，所以∠AS＜∠SAE；而∠SO＝∠SAE+∠AS，

故∠SO＜2∠SAE；

即∠SFO＜2∠SAE．故③正确．

故选：B．