Question

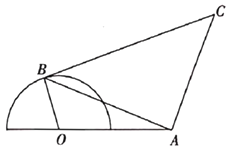
【题目】某生态农庄有一块如图所示的空地，其中半圆O的直径为300米，A为直径延长线上的点，米，B为半圆上任意一点，以AB为一边作等腰直角，其中BC为斜边．

若；，求四边形OACB的面积；

现决定对四边形OACB区域地块进行开发，将区域开发成垂钓中心，预计每平方米获利10元，将区域开发成亲子采摘中心，预计每平方米获利20元，则当为多大时，垂钓中心和亲子采摘中心获利之和最大？

Answer 1

【答案】(1)平方米；(2)

【解析】

计算时和的面积，求和得出四边形OABC的面积；

设，求出和的面积和，得出目标函数的解析式，再求该函数取得最大值时对应的值．

当时，

平方米；

在中，由余弦定理得，

；

平方米，

四边形OABC的面积为

平方米；

设，则，

所以，

在中，由余弦定理得，

；

，

不妨设垂钓中心和亲子中心获利之和为y元，

则有；

化简得；

因为，

所以当时，垂钓中心和亲子采摘中心获利之和最大．