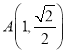题目内容
【题目】在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,则三棱锥
,则三棱锥![]() 外接球的体积的最小值为( )
外接球的体积的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由三角形全等可得∠ABD=∠ACD=90°,故而AD为棱锥外接球的直径,根据勾股定理得出AD关于AB的函数,求出AD的最小值即可得出答案.
∵AB=AC,DB=DC,AD为公共边,
∴△ABD≌△ACD,
又AB⊥BD,即∠ABD=90°,∴∠ACD=90°,
设AD的中点为O,则OA=OB=OD=OC,
∴O为棱锥A﹣BCD的外接球的球心.
∵AB+BD=4,∴AD2=AB2+(4﹣AB)2=2AB2﹣8AB+16=2(AB﹣2)2+8,
∴当AB=2时,AD2取得最小值8,即AD的最小值为2![]() ,
,
∴棱锥外接球的最小半径为![]() AD
AD![]() ,
,
∴外接球的最小体积为V![]() .
.
故选:C.

练习册系列答案
相关题目