题目内容
椭圆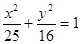 的左、右焦点分别为
的左、右焦点分别为 ,弦AB过
,弦AB过 ,若
,若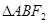 的内切圆周长为
的内切圆周长为 ,A,B两点的坐标分别为
,A,B两点的坐标分别为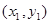 和
和 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
D
解析试题分析:由椭圆的标准方程可得: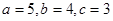 ,因为
,因为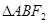 的内切圆周长为
的内切圆周长为 ,所以
,所以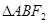 的内切圆的半径为
的内切圆的半径为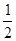 ,则根据三角形内切圆半径
,则根据三角形内切圆半径 和周长
和周长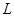 与三角形的面积
与三角形的面积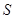 的关系有
的关系有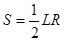 ,所以
,所以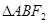 的面积为
的面积为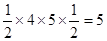 ,而
,而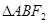 的面积又等于
的面积又等于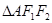 和
和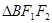 之和,即
之和,即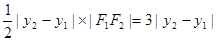 ,所以
,所以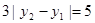 ,则
,则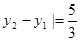 ,故选D.
,故选D.
考点:本题主要考查了直线与圆锥曲线的综合问题,椭圆的简单性质,三角形内切圆性质,本题的关键是求出△ABF2的面积,并考查了数形结合的思想方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知O为坐标原点,P是曲线 :
: 上到直线
上到直线 :
: 距离最小的点,且直线OP是双曲线
距离最小的点,且直线OP是双曲线 :
: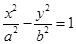
 的一条渐近线。则
的一条渐近线。则 与
与 的公共点个数是( )
的公共点个数是( )
| A.2 | B.1 |
| C.0 | D.不能确定,与 、 、 的值有关 的值有关 |
若直线 和⊙O∶
和⊙O∶ 相离,则过点
相离,则过点 的直线与椭圆
的直线与椭圆 的交点个数为( )
的交点个数为( )
| A.至多一个 | B. 2个 | C. 1个 | D.0个 |
已知抛物线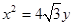 的准线过双曲线
的准线过双曲线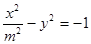 的一个焦点,则双曲线的离心率为( )
的一个焦点,则双曲线的离心率为( )
A.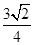 | B.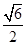 | C. | D.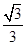 |
双曲线方程为 ,则它的右焦点坐标为( )
,则它的右焦点坐标为( )
A. | B. | C. | D. |
已知双曲线 的两条渐近线与以椭圆
的两条渐近线与以椭圆 的左焦点为圆心、半径为
的左焦点为圆心、半径为 的圆相切,则双曲线的离心率为( )
的圆相切,则双曲线的离心率为( )
A. | B. | C. | D. |
已知斜率为2的直线 双曲线
双曲线 交
交 两点,若点
两点,若点 是
是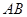 的中点,则
的中点,则 的离心率等于( )
的离心率等于( )
A.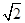 | B. | C.2 | D. |
 中,
中,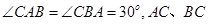 边上的高分别为
边上的高分别为 ,垂足分别是
,垂足分别是 ,则以
,则以 为焦点且过
为焦点且过 ,则
,则 的值为( )
的值为( )




 的左右焦点分别为
的左右焦点分别为 ,若椭圆
,若椭圆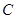 上恰好有6个不同的点
上恰好有6个不同的点 ,使得△F1F2P为等腰三角形,则椭圆
,使得△F1F2P为等腰三角形,则椭圆


