题目内容
【题目】如图,设点![]() 是抛物线
是抛物线![]() 的焦点,直线
的焦点,直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() (点
(点![]() 位于第一象限),并与抛物线
位于第一象限),并与抛物线![]() 的准线相交于点
的准线相交于点![]() .过点
.过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,连结
,连结![]() .
.
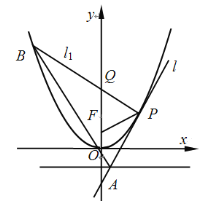
(1)证明:![]() 为等腰三角形;
为等腰三角形;
(2)求![]() 面积的最小值.
面积的最小值.
【答案】(1)证明见解析;(2)4
【解析】
(1)利用导数求出点P处的切线方程,由垂直关系写出法线方程,得到点Q坐标,由抛物线定义得到![]() ;
;
(2)先求出点A,B的坐标,再求![]() 与
与![]() 的表达式,利用直角三角形得到面积的函数关系,再求最大值.
的表达式,利用直角三角形得到面积的函数关系,再求最大值.
(1)设点P的坐标为![]() 且
且![]() ,
,
因为直线l与抛物线C相切,求导得![]() ,即
,即![]() ,
,
所以直线l的方程为:![]() ,
,
得直线m的方程为:![]() ,即
,即![]() ,
,
因为![]() ,即
,即![]() ,
,
而![]() ,
,
所以得![]() ,即
,即![]() 为等腰三角形.
为等腰三角形.
(或者求出切线与y轴的交点,可证点F为直角三角形斜边的中点,同样可证)
(2)因为抛物线C的准线为![]() ,得
,得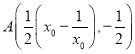 ,
,
所以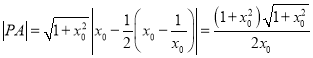 ,
,
联立方程组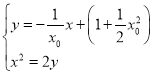 ,得
,得![]() ,
,
因为![]() ,
,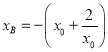 ,即
,即 ,
,
所以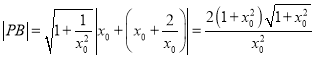 ,
,
得![]() 面积为
面积为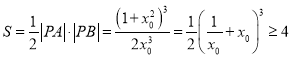 ,
,
当且仅当![]() 时,取到最小值4.
时,取到最小值4.

练习册系列答案
相关题目