Question

【题目】已知函数（且）的零点是.

（1）设曲线在零点处的切线斜率分别为，判断的单调性；

（2）设是的极值点，求证：.

Answer 1

【答案】（1）在单调递增，在递减（2）见解析

【解析】

（1）先求出函数的零点，，再利用导数的几何意义可得关于的函数，再利用导数研究函数的单调性即可；

（2）对函数进行求导得，利用导数证明函数，不妨设，利用所证不等式，即可证得结论.

由题可知：函数的定义域为

（1）由，得，.

则，，

所以.

令.则，

所以当时，；当时，

故在单调递增，在递减.

（2），

又在，恒成立，

由题知为的极值点，

所以且在单调递减，在单调递增，

故为的极小值点.

令，

则

，

故，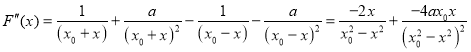

因为，所以，所以在单调递减，

所以

所以在单调递减，所以

所以，

不妨设，

所以，又在单调递减，在单调递增，

所以，即.