题目内容
【题目】已知函数![]() .(
.(![]() 是自然对数的底数)
是自然对数的底数)
(1)求![]() 的单调递减区间;
的单调递减区间;
(2)若函数![]() ,证明
,证明![]() 在
在![]() 上只有两个零点.(参考数据:
上只有两个零点.(参考数据:![]() )
)
【答案】(1)![]() (k∈Z).(2)见解析.
(k∈Z).(2)见解析.
【解析】
(1)由f'(x)<0得![]() ,利用正弦函数的单调性质可得f(x)的单调递减区间;
,利用正弦函数的单调性质可得f(x)的单调递减区间;
(2)依题意可得g'(x)=ex(sinx+cosx)﹣2,分析其单调情况并作出图象,利用零点存在性定理可得,g(x)在(x1,x2)和(x2,π)内各有一个零点,从而可证得结论成立.
(1)f(x)=exsinx,定义域为R.![]() .
.
由f'(x)<0得![]() ,解得
,解得![]() (k∈Z).
(k∈Z).
∴f(x)的单调递减区间为![]() (k∈Z).
(k∈Z).
(2)∵g'(x)=ex(sinx+cosx)﹣2,∴g'(x)=2excosx.
∵x∈(0,π),∴当![]() 时,g'(x)>0;当
时,g'(x)>0;当![]() 时,g'(x)<0.
时,g'(x)<0.
∴g'(x)在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
又∵g'(0)=1﹣2<0,![]() ,g'(π)=﹣eπ﹣2<0,
,g'(π)=﹣eπ﹣2<0,
∴g'(x)在(0,π)上图象大致如右图.
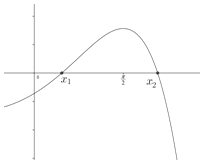
∴![]() ,
,![]() ,使得g'(x1)=0,g'(x2)=0,
,使得g'(x1)=0,g'(x2)=0,
且当x∈(0,x1)或x∈(x2,π)时,g'(x)<0;当x∈(x1,x2)时,g'(x)>0.
∴g(x)在(0,x1)和(x2,π)上单调递减,在(x1,x2)上单调递增.
∵g(0)=0,∴g(x1)<0.
∵![]() ,∴g(x2)>0,
,∴g(x2)>0,
又∵g(π)=﹣2π<0,由零点存在性定理得,g(x)在(x1,x2)和(x2,π)内各有一个零点,
∴函数g(x)在(0,π)上有两个零点.

练习册系列答案
相关题目