题目内容
【题目】已知定义在R上的函数f(x)=ex+mx2﹣m(m>0),当x1+x2=1时,不等式f(x1)+f(0)>f(x2)+f(1)恒成立,则实数x1的取值范围是( )
A.(﹣∞,0)
B.![]()
C.![]()
D.(1,+∞)
【答案】D
【解析】解:∵不等式f(x1)+f(0)>f(x2)+f(1)恒成立, ∴不等式f(x1)﹣f(x2)>f(1)﹣f(0)恒成立,
又∵x1+x2=1,
∴不等式f(x1)﹣f(1﹣x1)>f(1)﹣f(1﹣1)恒成立,
设g(x)=f(x)﹣f(1﹣x),
∵f(x)=ex+mx2﹣m(m>0),
∴g(x)=ex﹣e1﹣x+m(2x﹣1),
则g′(x)=ex+e1﹣x+2m>0,∴g(x)在R上单调递增,
∴不等式g(x1)>g(1)恒成立,
∴x1>1,
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
频数 | 20 | 40 | 80 | 50 | 10 | |
男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
频数 | 45 | 75 | 90 | 60 | 30 |
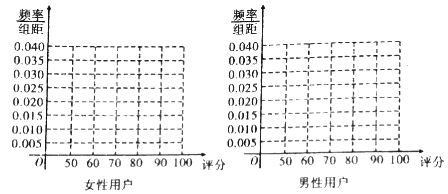
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取3名用户,求3名用户评分小于90分的人数的分布列和期望.