题目内容
【题目】某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图: 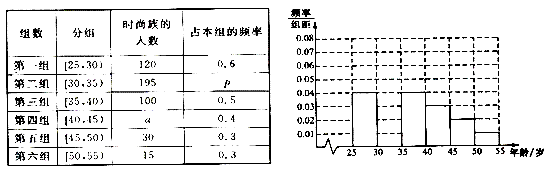
完成以下问题:
(Ⅰ)补全频率分布直方图并求n , a , p的值;
(Ⅱ)从[40,50)岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和期望E(X)..
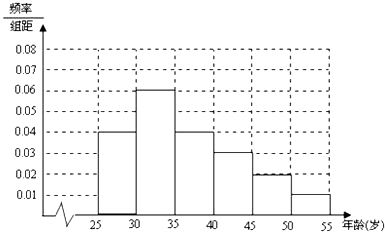
【答案】解:(Ⅰ)第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,
所以高为 ![]() . 频率直方图如下:
. 频率直方图如下:
第一组的人数为 ![]() ,频率为0.04×5=0.2,所以
,频率为0.04×5=0.2,所以 ![]() .
.
由题可知,第二组的频率为0.3,所以第二组的人数为1000×0.3=300, 所以 ![]() .
.
第四组的频率为0.03×5=0.15,所以第四组的人数为1000×0.15=150, 所以a=150×0.4=60.
(Ⅱ)因为[40,45)岁年龄段的“时尚族”与[45,50)岁年龄段的“时尚族”的比值
为60:30=2:1,所以采用分层抽样法抽取18人,[40,45)岁中有12人,[45,50)岁中有6人.
随机变量X服从超几何分布. ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
所以随机变量X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴数学期望 ![]() (或者
(或者 ![]() )
)
【解析】(1)根据题意结合已知条件可求出第二组的频率然后求出高的值画出频率的直方图即可求出第一组的人数和频率从而求出n的值,再根据第二组的频率以及人数求出p的值然后求出第四组的频率和人数进而求出a的值。(2)根据题意结合已知条件采用分层抽样法抽取18人,[40,45)岁中有12人,[45,50)岁中有6人,随机变量X的取值可能为0、1、2、3分别求出相应的概率,求出各个随机变量下的概率列出分布列,再根据数学期望公式代入数值求出结果即可,

【题目】计划在某水库建一座至多安装 ![]() 台发电机的水电站,过去
台发电机的水电站,过去 ![]() 年的水文资料显示,水库年入流量
年的水文资料显示,水库年入流量 ![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足 ![]() 的年份有
的年份有 ![]() 年,不低于
年,不低于 ![]() 且不超过
且不超过 ![]() 的年份有
的年份有 ![]() 年,超过
年,超过 ![]() 的年份有
的年份有 ![]() 年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来 ![]() 年中,设
年中,设 ![]() 表示流量超过
表示流量超过 ![]() 的年数,求
的年数,求 ![]() 的分布列及期望;
的分布列及期望;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量 ![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 | 1 |
|
|
若某台发电机运行,则该台年利润为 ![]() 万元,若某台发电机未运行,则该台年亏损
万元,若某台发电机未运行,则该台年亏损 ![]() 万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
【题目】为了了解青少年的肥胖是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
常喝 | 不常喝 | 总计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
总计 | 30 |
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为 ![]() .
.
(1)请将列联表补充完整;
(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ![]() ,其中n=a+b+c+d .
,其中n=a+b+c+d .