题目内容
求过点(2,0)且与曲线y=x3相切的直线方程.
y=0或27x-y-54=0
设切点坐标为(x0,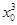 ),则由于y′=3x2,所以切线斜率为3
),则由于y′=3x2,所以切线斜率为3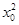 ,切线方程为y-
,切线方程为y-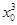 =3
=3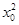 (x-x0),它过点(2,0),
(x-x0),它过点(2,0),
∴0-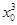 =3
=3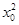 (2-x0)
(2-x0)
∴x0=0或x0=3.
若x0=0,则切点坐标为(0,0),切线方程为y=0.
若x0=3,则切点坐标为(3,27),切线方程为y-27=3×32(x-3),即27x-y-54=0.
所以,所求直线方程为y=0或27x-y-54=0
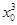 ),则由于y′=3x2,所以切线斜率为3
),则由于y′=3x2,所以切线斜率为3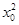 ,切线方程为y-
,切线方程为y-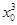 =3
=3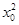 (x-x0),它过点(2,0),
(x-x0),它过点(2,0),∴0-
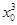 =3
=3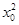 (2-x0)
(2-x0)∴x0=0或x0=3.
若x0=0,则切点坐标为(0,0),切线方程为y=0.
若x0=3,则切点坐标为(3,27),切线方程为y-27=3×32(x-3),即27x-y-54=0.
所以,所求直线方程为y=0或27x-y-54=0

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
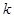 和
和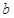 ,使得函数
,使得函数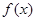 和
和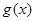 对其定义域上的任意实数
对其定义域上的任意实数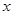 分别满足:
分别满足: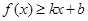 和
和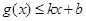 ,则称直线
,则称直线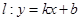 为
为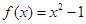 和函数
和函数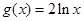 ,那么函数
,那么函数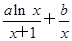 ,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0.求a,b.
,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0.求a,b. 处的切线方程为________.
处的切线方程为________.