题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,已知4sin2
-cos2C=
,且a+b=5,c=
,
求:
(1)∠C;
(2)△ABC的面积.
| A+B |
| 2 |
| 7 |
| 2 |
| 7 |
求:
(1)∠C;
(2)△ABC的面积.
(1)∵4sin2
-cos2C=
,
∴2[1-cos(A+B)]-2cos2C+1=
,
∴2+2cosC-2cos2C+1=
,
∴cos2C-cosC+
=0,∴cosC=
∵0<C<π,∴C=
(2)由余弦定理得:cosC=
=
,∴ab=a2+b2-7
∴3ab=(a+b)2-7,即ab=6
∴S△ABC=
absinC=
| A+B |
| 2 |
| 7 |
| 2 |
∴2[1-cos(A+B)]-2cos2C+1=
| 7 |
| 2 |
∴2+2cosC-2cos2C+1=
| 7 |
| 2 |
∴cos2C-cosC+
| 1 |
| 4 |
| 1 |
| 2 |
∵0<C<π,∴C=
| π |
| 3 |
(2)由余弦定理得:cosC=
| a2+b2-7 |
| 2ab |
| 1 |
| 2 |
∴3ab=(a+b)2-7,即ab=6
∴S△ABC=
| 1 |
| 2 |
3
| ||
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
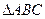 的面积是30,内角
的面积是30,内角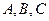 所对边长分别为
所对边长分别为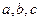 ,
,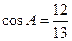 .
.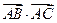 ;
;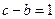 ,求
,求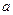 的值.
的值.
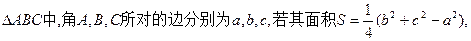
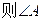 = .
= .