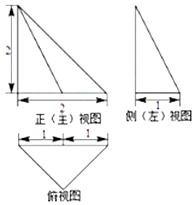
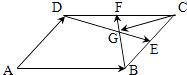
题目内容
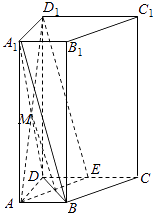
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC. 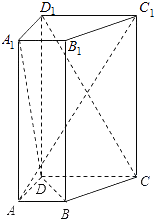
(1)求证:D1C⊥AC1;
(2)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.
【答案】
(1)证明:在直四棱柱ABCD﹣A1B1C1D1中,
连接C1D,∵DC=DD1,
∴四边形DCC1D1是正方形.∴DC1⊥D1C.
又AD⊥DC,AD⊥DD1,DC⊥DD1=D,
∴AD⊥平面DCC1D1,D1C平面DCC1D1,
∴AD⊥D1C.∵AD,DC1平面ADC1,
且AD⊥DC=D,∴D1C⊥平面ADC1,
又AC1平面ADC1,∴D1C⊥AC1
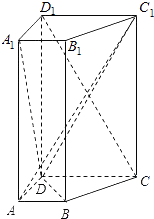
(2)解:连接AD1,连接AE,
设AD1∩A1D=M,BD∩AE=N,连接MN,∵平面AD1E∩平面A1BD=MN,
要使D1E∥平面A1BD,
须使MN∥D1E,
又M是AD1的中点.∴N是AE的中点.
又易知△ABN≌△EDN,∴AB=DE.
即E是DC的中点.
综上所述,当E是DC的中点时,可使D1E∥平面A1BD.
【解析】(1)要证D1C⊥AC1;需证D1C⊥平面ADC1即可(2)确定E的位置,使D1E∥平面A1BD,设AD1∩A1D=M,BD∩AE=N,连接MN,证明MN∥D1E即可.
【考点精析】利用空间中直线与平面之间的位置关系和直线与平面平行的性质对题目进行判断即可得到答案,需要熟知直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点;一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行.

【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
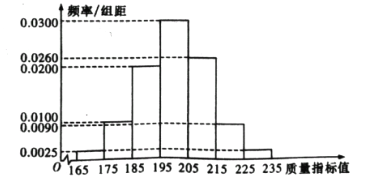
(1)根据以上抽样调查数据 ,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
分数区间 | 甲班频率 | 乙班频率 |
[0,30) | 0.1 | 0.2 |
[30,60) | 0.2 | 0.2 |
[60,90) | 0.3 | 0.3 |
[90,120) | 0.2 | 0.2 |
[120,150) | 0.2 | 0.1 |
(Ⅰ)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(Ⅱ)根据以上数据完成下面的2×2列联表:在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
优秀 | 不优秀 | 总计 | |
甲班 | |||
乙班 | |||
总计 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.