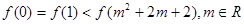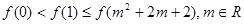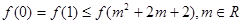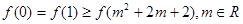题目内容
已知函数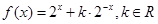 .
.
(I)若函数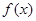 为奇函数,求实数
为奇函数,求实数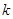 的值;
的值;
(II)若对任意的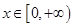 ,都有
,都有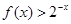 成立,求实数
成立,求实数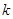 的取值范围.
的取值范围.
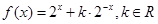 .
.(I)若函数
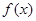 为奇函数,求实数
为奇函数,求实数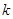 的值;
的值;(II)若对任意的
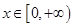 ,都有
,都有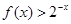 成立,求实数
成立,求实数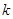 的取值范围.
的取值范围.(Ⅰ)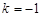 . (Ⅱ)
. (Ⅱ) .
.
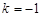 . (Ⅱ)
. (Ⅱ) .
.试题分析:(Ⅰ)根据
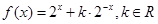 是奇函数,
是奇函数, ,得到恒等式
,得到恒等式 对一切
对一切 恒成立,不难得到
恒成立,不难得到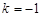 .
.(Ⅱ)由已知得到
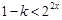 对
对 恒成立,从而只需
恒成立,从而只需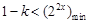 ,
,问题转化成求
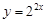 在
在 上的最小值,利用函数的单调性易得
上的最小值,利用函数的单调性易得 .
.试题解析:(Ⅰ)因为
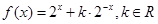 是奇函数,所以
是奇函数,所以 ,2分
,2分即
 所以
所以 对一切
对一切 恒成立,
恒成立, 所以
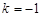 . 6分
. 6分(Ⅱ)因为
 ,均有
,均有 即
即 成立,
成立,所以
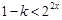 对
对 恒成立, 8分
恒成立, 8分所以
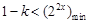 ,
,因为
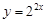 在
在 上单调递增,所以
上单调递增,所以 ,
,所以
 . 12分
. 12分
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
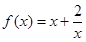 在[
在[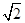 ,+∞)上的单调性.
,+∞)上的单调性.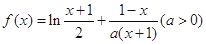 .
.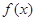 在
在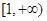 上为增函数, 求实数
上为增函数, 求实数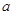 的取值范围;
的取值范围;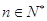 且
且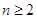 时,
时,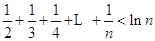 .
. 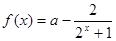 ,
,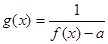 若函数
若函数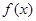 为奇函数,求
为奇函数,求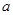 的值.
的值.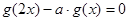 ,有唯一实数解,求
,有唯一实数解,求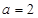 ,则是否存在实数
,则是否存在实数
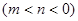 ,使得函数
,使得函数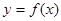 的定义域和值域都为
的定义域和值域都为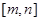 。若存在,求出
。若存在,求出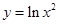 的图象可能是
的图象可能是 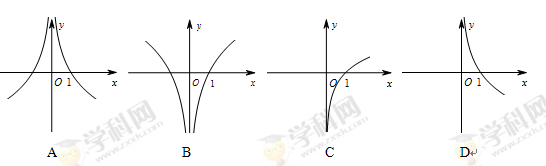
 ,当
,当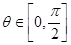 变化时,
变化时,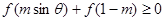 恒成立,则实数
恒成立,则实数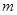 的取值范围是___________.
的取值范围是___________.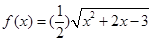 的增区间为 .
的增区间为 .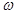 >0,若函数
>0,若函数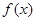 =sin
=sin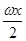 cos
cos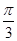 ,
,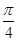 ]上单调递增,则
]上单调递增,则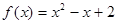 ,则下列关系中一定正确的是
,则下列关系中一定正确的是