题目内容
试判断函数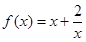 在[
在[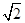 ,+∞)上的单调性.
,+∞)上的单调性.
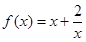 在[
在[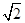 ,+∞)上的单调性.
,+∞)上的单调性.单调递增
试题分析:因为函数
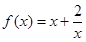 .所以由函数的单调性的定义来判断函数的单调性.通过自变量的大小的变化从而得到函数值的的大小变化.本小题关键是
.所以由函数的单调性的定义来判断函数的单调性.通过自变量的大小的变化从而得到函数值的的大小变化.本小题关键是 的正负的判断.由于
的正负的判断.由于 .所以可得
.所以可得 >0.本小题也可以通过求导数来证明.
>0.本小题也可以通过求导数来证明.试题解析:设
 ,则有
,则有
 =
=
=
 =
= =
= .
.
 ,
, 且
且 ,
, ,
,所以
 ,即
,即 .所以函数
.所以函数 在区间[
在区间[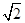 ,+∞)上单调递增.
,+∞)上单调递增.
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
题目内容
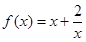 在[
在[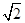 ,+∞)上的单调性.
,+∞)上的单调性.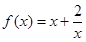 .所以由函数的单调性的定义来判断函数的单调性.通过自变量的大小的变化从而得到函数值的的大小变化.本小题关键是
.所以由函数的单调性的定义来判断函数的单调性.通过自变量的大小的变化从而得到函数值的的大小变化.本小题关键是 的正负的判断.由于
的正负的判断.由于 .所以可得
.所以可得 >0.本小题也可以通过求导数来证明.
>0.本小题也可以通过求导数来证明. ,则有
,则有
 =
=
 =
= =
= .
.
 ,
, 且
且 ,
, ,
, ,即
,即 .所以函数
.所以函数 在区间[
在区间[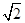 ,+∞)上单调递增.
,+∞)上单调递增.
 全优点练单元计划系列答案
全优点练单元计划系列答案