题目内容
(本小题12分)
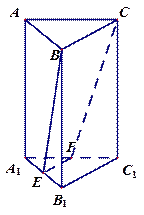
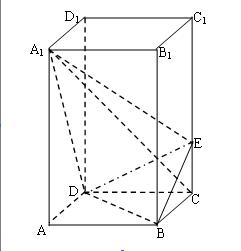
正三棱柱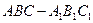 中,所有棱长均相等,
中,所有棱长均相等,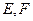 分别是棱
分别是棱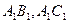 的中点,
的中点,
截面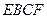 将三棱柱截成几何体Ⅰ和几何体Ⅱ两个几何体.
将三棱柱截成几何体Ⅰ和几何体Ⅱ两个几何体.
 ①求几何体Ⅰ和几何体Ⅱ的表面积之比;
①求几何体Ⅰ和几何体Ⅱ的表面积之比;
②求几何体Ⅰ和几何体Ⅱ的体积之比.
正三棱柱
 中,所有棱长均相等,
中,所有棱长均相等,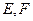 分别是棱
分别是棱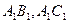 的中点,
的中点,截面
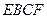 将三棱柱截成几何体Ⅰ和几何体Ⅱ两个几何体.
将三棱柱截成几何体Ⅰ和几何体Ⅱ两个几何体. ①求几何体Ⅰ和几何体Ⅱ的表面积之比;
①求几何体Ⅰ和几何体Ⅱ的表面积之比;②求几何体Ⅰ和几何体Ⅱ的体积之比.
⑴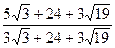 ;(2)
;(2)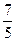
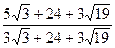 ;(2)
;(2)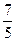
略

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
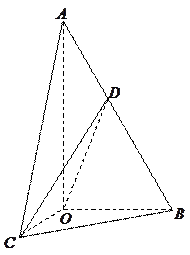
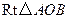 中,
中,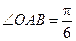 ,斜边
,斜边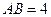 .
.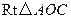 可以通过
可以通过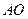 为轴旋转得到,且二面角
为轴旋转得到,且二面角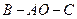 是直二面角.动点
是直二面角.动点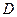 的斜边
的斜边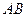 上.
上.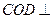 平面
平面 ;
;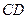 所成角的大小;
所成角的大小;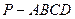 中,
中,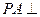 底面
底面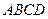 ,
,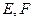 分
分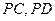 的中点,求证:
的中点,求证: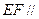 平面
平面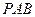 ;
;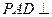 平面
平面 .
.
 中,
中,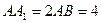 ,点
,点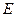 在
在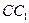 上且
上且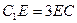 .
.
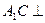 平面
平面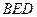 ;
;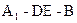 的余弦值.
的余弦值.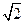 .
.
