题目内容
(本小题共14分)
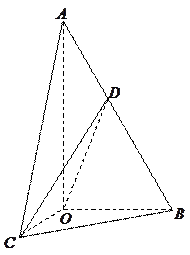
如图,在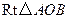 中,
中,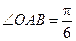 ,斜边
,斜边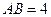 .
.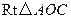 可以通过
可以通过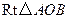 以直线
以直线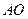 为轴旋转得到,且二面角
为轴旋转得到,且二面角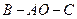 是直二面角.动点
是直二面角.动点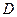 的斜边
的斜边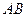 上.
上.
(I)求证:平面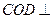 平面
平面 ;
;
(II)当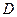 为
为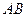 的中点时,求异面直线
的中点时,求异面直线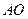 与
与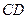 所成角的大小;
所成角的大小;
(III)求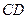 与平面
与平面 所成角的最大值.
所成角的最大值.
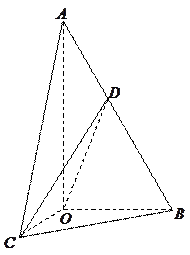
如图,在
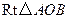 中,
中,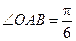 ,斜边
,斜边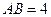 .
.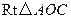 可以通过
可以通过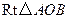 以直线
以直线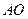 为轴旋转得到,且二面角
为轴旋转得到,且二面角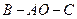 是直二面角.动点
是直二面角.动点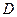 的斜边
的斜边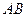 上.
上.(I)求证:平面
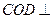 平面
平面 ;
;(II)当
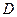 为
为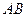 的中点时,求异面直线
的中点时,求异面直线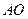 与
与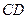 所成角的大小;
所成角的大小;(III)求
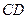 与平面
与平面 所成角的最大值.
所成角的最大值.(I)平面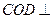 平面
平面
(II)异面直线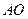 与
与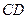 所成角的大小为
所成角的大小为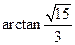
(III)CD与平面 所成角的最大值为
所成角的最大值为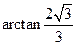
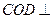 平面
平面
(II)异面直线
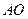 与
与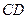 所成角的大小为
所成角的大小为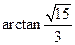
(III)CD与平面
 所成角的最大值为
所成角的最大值为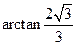
解法一:
(I)由题意,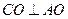 ,
, ,
,
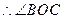 是二面角
是二面角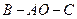 是直二面角,
是直二面角,
又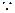 二面角
二面角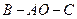 是直二面角,
是直二面角,
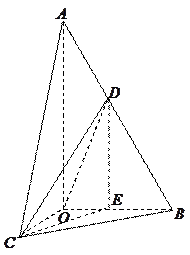
 ,又
,又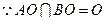 ,
,
 平面
平面 ,
,
又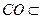 平面
平面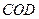 .
.
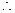 平面
平面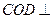 平面
平面 .
.
(II)作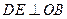 ,垂足为
,垂足为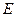 ,连结
,连结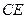 (如图),则
(如图),则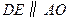 ,
,
 是异面直线
是异面直线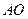 与
与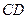 所成的角.
所成的角.
在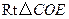 中,
中,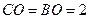 ,
, ,
,
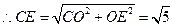 .
.
又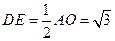 .
.
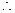 在
在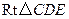 中,
中,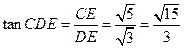 .
.
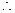 异面直线
异面直线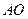 与
与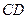 所成角的大小为
所成角的大小为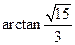 .
.
(III)由(I)知,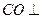 平面
平面 ,
,
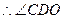 是
是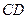 与平面
与平面 所成的角,且
所成的角,且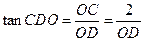 .
.
当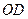 最小时,
最小时,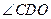 最大,
最大,
这时,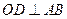 ,垂足为
,垂足为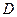 ,
,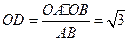 ,
, ,
,
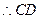 与平面
与平面 所成角的最大值为
所成角的最大值为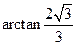 .
.
解法二:
(I)同解法一.
 (II)建立空间直角坐标系
(II)建立空间直角坐标系 ,如图,则
,如图,则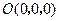 ,
,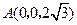 ,
,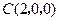 ,
, ,
,
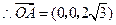 ,
,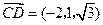 ,
,
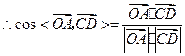
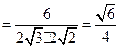 .
.
 异面直线
异面直线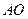 与
与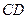 所成角的大小为
所成角的大小为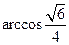 .
.
(III)同解法一
(I)由题意,
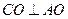 ,
, ,
,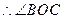 是二面角
是二面角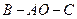 是直二面角,
是直二面角,又
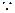 二面角
二面角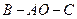 是直二面角,
是直二面角,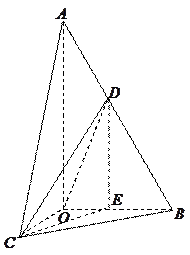
 ,又
,又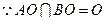 ,
, 平面
平面 ,
,又
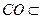 平面
平面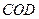 .
.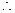 平面
平面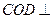 平面
平面 .
.(II)作
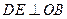 ,垂足为
,垂足为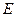 ,连结
,连结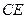 (如图),则
(如图),则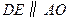 ,
, 是异面直线
是异面直线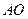 与
与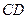 所成的角.
所成的角.在
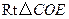 中,
中,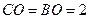 ,
, ,
,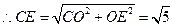 .
.又
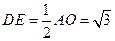 .
.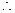 在
在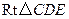 中,
中,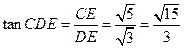 .
. 异面直线
异面直线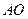 与
与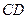 所成角的大小为
所成角的大小为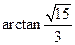 .
.(III)由(I)知,
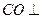 平面
平面 ,
,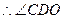 是
是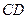 与平面
与平面 所成的角,且
所成的角,且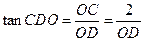 .
.当
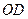 最小时,
最小时,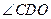 最大,
最大,这时,
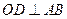 ,垂足为
,垂足为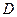 ,
,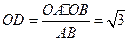 ,
, ,
,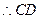 与平面
与平面 所成角的最大值为
所成角的最大值为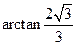 .
.解法二:
(I)同解法一.
 (II)建立空间直角坐标系
(II)建立空间直角坐标系 ,如图,则
,如图,则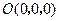 ,
,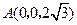 ,
,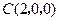 ,
, ,
,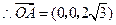 ,
,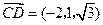 ,
,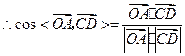
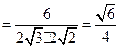 .
. 异面直线
异面直线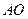 与
与 所成角的大小为
所成角的大小为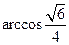 .
.(III)同解法一

练习册系列答案
相关题目
 中,
中,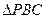 为正三角形,
为正三角形, ,
, 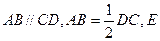 为
为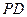 中点
中点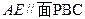 ;(2)求证:
;(2)求证:
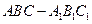 中,
中,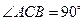 ,
,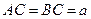 ,
,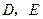 分别为棱
分别为棱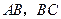 的中点,
的中点,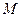 为棱
为棱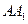 上的点,二面角
上的点,二面角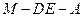 为
为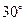 .
.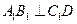 ;
;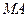 的长,并求点
的长,并求点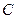 到平面
到平面 的距离.
的距离.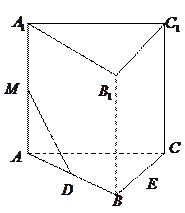
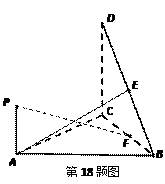
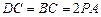 ,
,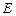 为DB的中点,
为DB的中点,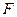 是线段
是线段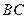 上的动点,设平面
上的动点,设平面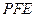 与平面
与平面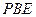 所成的平面角大小为
所成的平面角大小为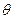 ,当
,当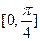 内取值时,求直线PF与平面DBC所成的角的范围。
内取值时,求直线PF与平面DBC所成的角的范围。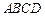 中,
中,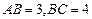 ,沿对角线
,沿对角线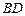 将
将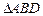 折起到
折起到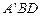 的位置,且
的位置,且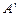 在平面
在平面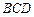 内的射影
内的射影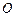 落在
落在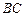 边上,则二面角
边上,则二面角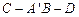 的平面角的正弦值为( )
的平面角的正弦值为( )

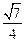
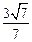
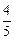
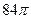 ,则圆台较小底面的半径为( )
,则圆台较小底面的半径为( )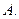 7
7  . 6
. 6 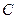 . 5
. 5 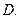 3
3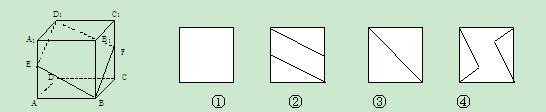
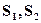 ,则
,则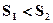
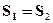
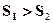
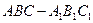 中,所有棱长均相等,
中,所有棱长均相等,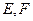 分别是棱
分别是棱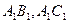 的中点,
的中点,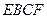 将三棱柱截成几何体Ⅰ和几何体Ⅱ两个几何体.
将三棱柱截成几何体Ⅰ和几何体Ⅱ两个几何体.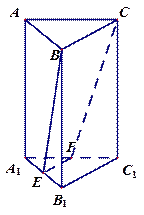 ①求几何体Ⅰ和几何体Ⅱ的表面积之比;
①求几何体Ⅰ和几何体Ⅱ的表面积之比;