题目内容
已知数列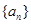 的各项均为正数,记
的各项均为正数,记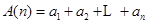 ,
,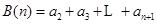 ,
,
 .
.
(1)若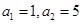 ,且对任意
,且对任意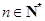 ,三个数
,三个数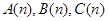 组成等差数列,求数列
组成等差数列,求数列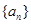 的通项公式.
的通项公式.
(2)证明:数列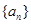 是公比为
是公比为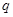 的等比数列的充分必要条件是:对任意
的等比数列的充分必要条件是:对任意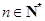 ,三个数
,三个数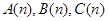 组成公比为
组成公比为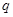 的等比数列.
的等比数列.
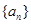 的各项均为正数,记
的各项均为正数,记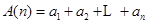 ,
,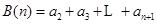 ,
, .
.(1)若
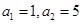 ,且对任意
,且对任意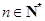 ,三个数
,三个数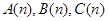 组成等差数列,求数列
组成等差数列,求数列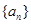 的通项公式.
的通项公式.(2)证明:数列
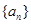 是公比为
是公比为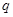 的等比数列的充分必要条件是:对任意
的等比数列的充分必要条件是:对任意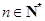 ,三个数
,三个数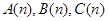 组成公比为
组成公比为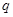 的等比数列.
的等比数列.(1) ;(2)详见解析
;(2)详见解析
 ;(2)详见解析
;(2)详见解析试题分析:(1)由三个数
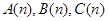 是等差数列,可得
是等差数列,可得 .根据定义可知即
.根据定义可知即 。变形为
。变形为  ,由等差数列的定义可知,数列
,由等差数列的定义可知,数列 是首项为1,公差为4的等差数列。从而可得其通项公式。(2)若对于任意
是首项为1,公差为4的等差数列。从而可得其通项公式。(2)若对于任意 ,三个
,三个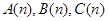 组成公比为
组成公比为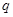 的等比数列,则
的等比数列,则 ,由
,由 得
得 将上式变形整理根据等比数列的定义可证得数列
将上式变形整理根据等比数列的定义可证得数列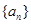 是公比为
是公比为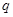 的等比数列;若数列
的等比数列;若数列 是公比为
是公比为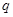 的等比数列,则对任意
的等比数列,则对任意 ,有
,有 .根据已知可证得
.根据已知可证得 =
= ,从而三个数
,从而三个数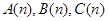 组成公比为
组成公比为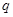 的等比数列.
的等比数列.解: (1)因为对任意
 ,三个数
,三个数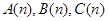 是等差数列,
是等差数列,所以
 . 1分
. 1分所以
 , 2分
, 2分即
 . 3分
. 3分所以数列
 是首项为1,公差为4的等差数列. 4分
是首项为1,公差为4的等差数列. 4分所以
 . 5分
. 5分(2)(1)充分性:若对于任意
 ,三个数
,三个数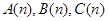 组成公比为
组成公比为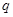 的等比数列,则
的等比数列,则 . 6分
. 6分所以
 得
得
即
 . 7分
. 7分因为当
 时,由
时,由 可得
可得 , 8分
, 8分所以
 .
.因为
 ,
,所以
 .
. 即数列
 是首项为
是首项为 ,公比为
,公比为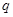 的等比数列, 9分
的等比数列, 9分(2)必要性:若数列
 是公比为
是公比为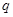 的等比数列,则对任意
的等比数列,则对任意 ,有
,有 . 10分
. 10分因为
 ,
,所以
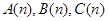 均大于
均大于 .于是
.于是 11分
11分 12分
12分即
 =
= =
=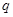 ,所以三个数
,所以三个数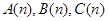 组成公比为
组成公比为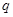 的等比数列. 13分
的等比数列. 13分综上所述,数列
 是公比为
是公比为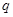 的等比数列的充分必要条件是:对任意n∈N﹡,三个数
的等比数列的充分必要条件是:对任意n∈N﹡,三个数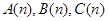 组成公比为
组成公比为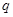 的等比数列. 14分
的等比数列. 14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和
和 的通项公式分别为
的通项公式分别为 ,
, .将
.将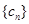 .
. ,
, ,
, ,
, 的值,并由此归纳数列
的值,并由此归纳数列 .
. 成等比数列,则
成等比数列,则 也成等比数列;②若数列{
也成等比数列;②若数列{ }既是等差数列也是等比数列,则{
}既是等差数列也是等比数列,则{ ,且
,且 ,则{
,则{ ,其中正确判断的序号是______.(注:把你认为正确判断的序号都填上)
,其中正确判断的序号是______.(注:把你认为正确判断的序号都填上) ,且
,且 按某种顺序排列成等差数列.
按某种顺序排列成等差数列. 的值;
的值; 的首项和公差都为
的首项和公差都为 的首项和公比都为
的首项和公比都为 项和分别为
项和分别为 ,且
,且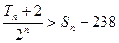 ,求满足条件的自然数
,求满足条件的自然数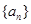 中,
中,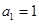 ,
,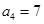 ,则公差
,则公差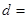 _____;
_____;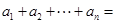 ____.
____. 满足:
满足: ,且对任意的m,n∈N*都有:
,且对任意的m,n∈N*都有: ,则
,则 ( )
( )


