题目内容
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下:
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
(1)元件A为正品的概率为 ,元件B为正品的概率为
,元件B为正品的概率为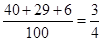 ;(2)(i)
;(2)(i)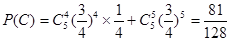 ;(ii)
;(ii)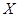 的分布列为:
的分布列为: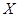
150 90 30 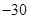
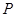

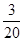
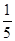
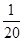
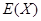
 .
.
解析试题分析:(1)用指标大于或等于82所对应的的元件的个数除以总的元件个数即是正品的概率;(2)(i)先设生产的5件元件中正品件数为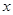 ,次品
,次品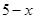 件,由题意列出不等式
件,由题意列出不等式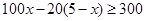 ,求解并确定
,求解并确定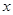 的取值是4或5,然后再由
的取值是4或5,然后再由 次独立重复试验某事件恰好发生
次独立重复试验某事件恰好发生 次的概率公式即可得到“生产5件元件B所获得的利润不少于300元”的概率;(ii)根据题意分别求出一件A正品和一件B正品,一件A次品和一件B正品,一件A正品和一件B次品,一件A次品和一件B次品的概率,列出分布列,由公式
次的概率公式即可得到“生产5件元件B所获得的利润不少于300元”的概率;(ii)根据题意分别求出一件A正品和一件B正品,一件A次品和一件B正品,一件A正品和一件B次品,一件A次品和一件B次品的概率,列出分布列,由公式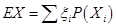 求出数学期望即可.
求出数学期望即可.
试题解析:(1)由题可知元件A为正品的概率为 ,元件B为正品的概率为
,元件B为正品的概率为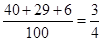 .
.
(2)(i)设生产的5件元件中正品件数为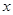 ,则有次品
,则有次品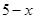 件,由题意知
件,由题意知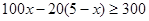 得到
得到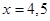 ,设“生产5件元件B所获得的利润不少于300元”为事件
,设“生产5件元件B所获得的利润不少于300元”为事件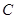 ,则
,则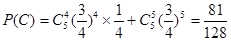
(ii)随机变量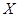 的所有取值为150,90,30,
的所有取值为150,90,30,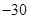
则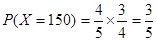 ,
,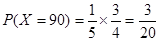 ,
,
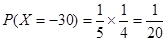
所以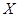 的分布列为:
的分布列为: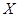
150 90 30 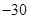
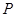

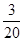
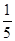
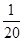
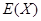
 .
.
考点:1. 次独立重复试验某事件恰好发生
次独立重复试验某事件恰好发生 次的概率;2.随机变量的分布列;3.数学期望.
次的概率;2.随机变量的分布列;3.数学期望.

2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |

经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出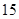 条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
罗非鱼的汞含量(ppm)
 | 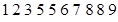 |
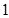 | 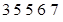 |
《中华人民共和国环境保护法》规定食品的汞含量不得超过
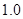 ppm.
ppm.(1)检查人员从这
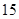 条鱼中,随机抽出
条鱼中,随机抽出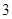 条,求
条,求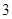 条中恰有
条中恰有 条汞含量超标的概率;
条汞含量超标的概率;(2)若从这批数量很大的鱼中任选
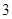 条鱼,记
条鱼,记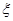 表示抽到的汞含量超标的鱼的条数.以此
表示抽到的汞含量超标的鱼的条数.以此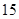 条鱼的样本数据来估计这批数量很大的鱼的总体数据,求
条鱼的样本数据来估计这批数量很大的鱼的总体数据,求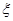 的分布列及数学期望
的分布列及数学期望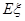 .
.  三个社区参加社会实践,要求每个社区至少有一名同学.
三个社区参加社会实践,要求每个社区至少有一名同学. 社区的概率;
社区的概率; 为四名同学中到
为四名同学中到 的值.
的值. .
. ,求
,求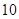 个同样型号的产品中,有
个同样型号的产品中,有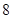 个是正品,
个是正品,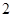 个是次品,从中任取
个是次品,从中任取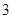 个,求(1)其中所含次品数
个,求(1)其中所含次品数 的期望、方差;(2)事件“含有次品”的概率。
的期望、方差;(2)事件“含有次品”的概率。