题目内容
从5名男生和3名女生中任选3人参加奥运会火炬接力活动.若随机变量X表示所选3人中女生的人数,求X的分布表及P(X<2).
X的分布表为X 0 1 2 3 P 



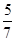
解析解:由题意分析可知,随机变量X服从超几何分布,其中N=8,M=3,n=3.
所以P(X=0)=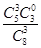 =
= ;P(X=1)=
;P(X=1)= =
= ;
;
P(X=2)= =
= ;P(X=3)=
;P(X=3)=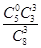 =
= .
.
从而随机变量X的分布表为
所以P(X<2)=P(X=0)+P(X=1)=X 0 1 2 3 P 



 +
+ =
=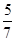 .
.

练习册系列答案
相关题目
某商店试销某种商品20天,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 频数 | 1 | 5 | 9 | 5 |
(1)求当天商店不进货的概率;
(2)记X为第二天开始营业时该商品视为件数,求X的分布列和数学期望.
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下:
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
第17届亚运会将于2014年9月18日至10月4日在韩国仁川进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱.
(1)根据调查数据制作2×2列联表;
(2)根据列联表的独立性检验,能否认为性别与喜爱运动有关?
| 参考数据 | 当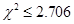 时,无充分证据判定变量 时,无充分证据判定变量 有关联,可以认为两变量无关联; 有关联,可以认为两变量无关联; |
当 时,有 时,有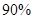 把握判定变量 把握判定变量 有关联; 有关联; | |
当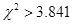 时,有 时,有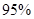 把握判定变量 把握判定变量 有关联; 有关联; | |
当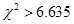 时,有 时,有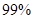 把握判定变量 把握判定变量 有关联. 有关联. |
 ,其中
,其中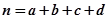 .)
.) 为了提高食品的安全度,某食品安检部门调查了一个海水养殖场的养殖鱼的有关情况,安检人员从这个海水养殖场中不同位置共捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据进行统计得下表.若规定超过正常生长速度(1.0~1.2 kg/年)的比例超过15%,则认为所饲养的鱼有问题,否则认为所饲养的鱼没有问题.
| 鱼的 质量 | [1.00, 1.05) | [1.05, 1.10) | [1.10, 1.15) | [1.15, 1.20) | [1.20, 1.25) | [1.25, 1.30) |
| 鱼的 条数 | 3 | 20 | 35 | 31 | 9 | 2 |
(2)上面捕捞的100条鱼中间,从质量在[1.00,1.05)和[1.25,1.30)的鱼中,任取2条鱼来检测,求恰好所取得的鱼的质量在[1.00,1.05)和[1.25,1.30)各有1条的概率.
 V”的事件为X,求概率P(X);
V”的事件为X,求概率P(X);