题目内容
20.已知数列{an}的前n项和为Sn,且2Sn+3=3an(n∈N*).(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=(n+1)log${\;}_{\sqrt{3}}$an,记Tn=$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$,求证:2Tn<1.
分析 (I)通过令n=1可得首项a1=3,当n≥2时,利用2Sn+3=3an与2Sn-1+3=3an-1的差可得公比,进而可得结论;
(II)通过bn=2n(n+1),分离分母可得$\frac{1}{{b}_{n}}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+1}$),并项相加即得结论.
解答 (I)解:当n=1时,2S1+3=2a1+3=3a1,得a1=3,
当n≥2时,2Sn+3=3an …①
2Sn-1+3=3an-1 …②
①-②,得:2an=3an-3an-1,即an=3an-1,
∴数列{an}为公比为3,首项为3的等比数列,
∴an=3•3n-1=3n(n∈N*);
(II)证明:∵bn=(n+1)log${\;}_{\sqrt{3}}$3n=2n(n+1),
∴$\frac{1}{{b}_{n}}$=$\frac{1}{2n(n+1)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+1}$),
∴Tn=$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$
=$\frac{1}{2}$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{n+1}$)
<$\frac{1}{2}$,
∴2Tn<1.
点评 本题考查求数列的通项和前n项和的取值范围,注意解题方法的积累,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.i为虚数单位,(1+i)$\overline{z}$=(1-i)2,则|z|=( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
15.已知a,b是实数,则“a>|b|”是“a2>b2”的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
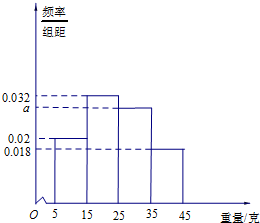 测量马口鱼性成熟时重量,从大量马口鱼中随机抽取100尾作为样本,测出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到重量样本的频率分布直方图,如图.
测量马口鱼性成熟时重量,从大量马口鱼中随机抽取100尾作为样本,测出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到重量样本的频率分布直方图,如图. 一个由若干行数字组成的数表,从第二行起,每一行中的数字均等于其肩上两个数字之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行,则最后一行的数是101×298.
一个由若干行数字组成的数表,从第二行起,每一行中的数字均等于其肩上两个数字之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行,则最后一行的数是101×298.